（本小题满分12分）如图1所示，直角梯形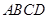
，
，
，
，
、
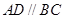为线段
、
上的点，且
，设
，沿
将梯形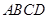翻折，使平面
平面
（如图2所示）．
（1）若以
、
、
、为顶点的三棱锥体积记为
，求的最大值及取最大值时的位置；
（2）在（1）的条件下，试在线段上的确定一点
使得
，并求直线
与平面
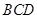所成的角
的正弦值．
有最大值
，试求实数
的值.
为减函数，
对
恒成立，求实数m的取值范围.
，且
，
. 
，有
.
，
的图象.
，求函数y＝
＋
，x∈
的最大值与最小值．相关知识点
推荐套卷
（本小题满分12分）如图1所示，直角梯形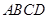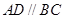，，，，、为线段、上的点，且，设，沿将梯形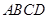翻折，使平面平面（如图2所示）．
（1）若以、、、为顶点的三棱锥体积记为，求的最大值及取最大值时的位置；
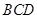（2）在（1）的条件下，试在线段上的确定一点使得，并求直线与平面所成的角的正弦值．
粤公网安备 44130202000953号