高中数学表面展开图试题

如图所示，圆锥的轴截面为等腰直角，为底面圆周上一点.

（1）若的中点为，,
求证：平面；
（2）如果,,求此圆锥的全面积.

在棱长为1的正方体中，点，分别是线段，（不包括端点）上的动点，且线段平行于平面，则四面体的体积的最大值是_______

如图，在中，，，是上的高，沿把折起，使.

（1）证明：平面平面；
（2）设，求三棱锥的体积.

如图，四棱锥中，底面是菱形，，，,,,是的中点，上的点满足．

（Ⅰ）求证：平面；
（Ⅱ）求三棱锥的体积．

如图，在四棱锥中，底面是正方形，底面，，点是的中点，，交于点．

（1）求证：平面平面；
（2）求三棱锥的体积．

如图，四边形ABCD为矩形，四边形ADEF为梯形，AD//FE，∠AFE=60º，且平面ABCD⊥平面ADEF，AF=FE=AB==2，点G为AC的中点．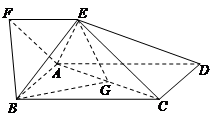

（Ⅰ）求证：EG//平面ABF；
（Ⅱ）求三棱锥B-AEG的体积；
（Ⅲ）试判断平面BAE与平面DCE是否垂直？若垂直，请证明；若不垂直，请说明理由．

如图，已知平面，四边形是矩形，，，点，分别是，的中点．

（Ⅰ）求三棱锥的体积；
（Ⅱ）求证：平面；
（Ⅲ）若点为线段中点，求证：∥平面．

如图所示，圆柱的高为2，底面半径为,AE、DF是圆柱的两条母线，过作圆柱的截面交下底面于,四边形ABCD是正方形.

（Ⅰ）求证；
（Ⅱ）求四棱锥E-ABCD的体积.

如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE和CF的中点.

（Ⅰ）求证：AC⊥平面BDEF；
（Ⅱ）求证：平面BDGH//平面AEF；
（Ⅲ）求多面体ABCDEF的体积.

如图，在三棱柱中，四边形为菱形，，四边形为矩形，若，，.

（1）求证：平面；
（2）求证：面；
（3）求三棱锥的体积.

如图，长方体中，为线段的中点,.

(Ⅰ)证明：⊥平面；
(Ⅱ)求点到平面的距离.

若正方体的外接球的体积为，则球心到正方体的一个面的距离为（）

A．1

B．2

C．3

D．4

如图，在三棱柱中，AC⊥BC，AB⊥，，D为AB的中点，且CD⊥。

（Ⅰ）求证：平面⊥平面ABC；
（2）求多面体的体积。

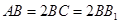如图，在长方体中，, 沿平面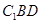把这个长方体截成两个几何体: 几何体（1）；几何体（2）

（I）设几何体（1）、几何体（2）的体积分为是、，求与的比值
(II)在几何体（2）中，求二面角的正切值

如图在长方体中，，，，点为的中点，点为的中点．

（1）求长方体的体积；
（2）若，，，求异面直线与所成的角．