有下列四个命题:
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若 有实根则
有实根则 ”;
”;
④“若 ”的逆否命题.
”的逆否命题.
其中真命题个数为 .
| A.1 | B.2 | C.3 | D.4 |
在下列命题中,
①两个复数不能比较大小;
②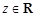 的一个充要条件是z与它的共轭复数相等。
的一个充要条件是z与它的共轭复数相等。
③若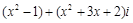 是纯虚数,则实数
是纯虚数,则实数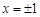 ;
;
④若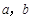 是两个相等的实数,则
是两个相等的实数,则 是纯虚数;
是纯虚数;
其中真命题的序号为 .
下列4个命题:
①“如果 ,则
,则 、
、 互为相反数”的逆命题
互为相反数”的逆命题
②“如果 ,则
,则 ”的否命题
”的否命题
③在△ABC中,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
④“函数 为奇函数”的充要条件是“
为奇函数”的充要条件是“ ”
”
其中真命题的序号是 .
下列四个命题:
①命题“若 ,则
,则 ”的否命题是“若
”的否命题是“若 ,则
,则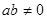 ”;
”;
②若命题 ,则
,则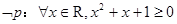 ;
;
③若命题“ ”与命题“
”与命题“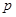 或
或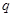 ”都是真命题,则命题
”都是真命题,则命题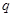 一定是真命题;
一定是真命题;
④命题“若 ,则
,则 ”是真命题.
”是真命题.
其中正确命题的序号是 .(把所有正确的命题序号都填上)
已知命题p:m∈R,且m+1≤0,命题q:∀x∈R,x2+mx+1>0恒成立,若p∧q为假命题,则m的取值范围是________.
下列四种说法:
①命题“ ,使得
,使得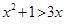 ”的否定是“
”的否定是“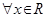 ,都有
,都有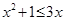 ”;
”;
②设 、
、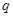 是简单命题,若“
是简单命题,若“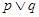 ”为假命题,则“
”为假命题,则“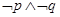 ” 为真命题;
” 为真命题;
③若 是
是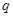 的充分不必要条件,则
的充分不必要条件,则 的必要不充分条件;
的必要不充分条件;
④把函数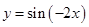
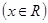 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数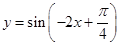
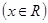 的图像.
的图像.
其中所有正确说法的序号是 .
命题“若 ,则
,则 (
( R)”否命题的真假性为 (从“真”、“假”中选填一个).
R)”否命题的真假性为 (从“真”、“假”中选填一个).
用反证法证明某命题时,对结论“自然数 中至多有2个偶数”的正确假设为“假设自然数
中至多有2个偶数”的正确假设为“假设自然数 中 ”.
中 ”.
、对于函数 与函数
与函数 有下列命题:
有下列命题:
①无论函数 的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
②函数 的图像与两坐标轴及其直线
的图像与两坐标轴及其直线 所围成的封闭图形的面积为4;
所围成的封闭图形的面积为4;
③方程 有两个根;
有两个根;
④函数 图像上存在一点处的切线斜率小于0;
图像上存在一点处的切线斜率小于0;
⑤若函数 在点P处的切线平行于函数
在点P处的切线平行于函数 在点Q处的切线,则直线PQ的斜率为
在点Q处的切线,则直线PQ的斜率为 ,其中正确的命题是________.(把所有正确命题的序号都填上)
,其中正确的命题是________.(把所有正确命题的序号都填上)