高中数学截面及其作法填空题

命题“若则”的逆命题是         .

在直角坐标系内，点实施变换后，对应点为，给出以下命题：
①圆上任意一点实施变换后，对应点的轨迹仍是圆
；
②若直线上每一点实施变换后，对应点的轨迹方程仍是则；
③椭圆上每一点实施变换后，对应点的轨迹仍是离心率不变的椭圆；
④曲线：上每一点实施变换后，对应点的轨迹是曲线，是曲线上的任意一点，是曲线上的任意一点，则的最小值为．
以上正确命题的序号是________（写出全部正确命题的序号）

给出下列四个命题，其中不正确命题的序号是            。
①若；②函数的图象关于x=对称；③函数为偶函数，④函数是周期函数，且周期为2。

有下列命题中假命题的序号是                 
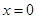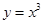①是函数的极值点；
②三次函数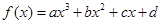有极值点的充要条件是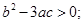
③奇函数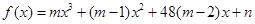在区间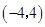上单调递减.
④若双曲线的渐近线方程为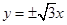，则其离心率为2.

命题“”的否定是         ．

命题“对任何”的否定是_________.

给出下列结论：
①设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则α⊥β是a⊥b的必要不充分条件．
②在区间[－1，1]上随机取一个数x，则的值介于0到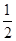之间的概率为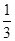
③从以正方体的顶点连线所成的直线中任取两条，则所取两条直线为异面直线的概率为 
④将4个相同的红球和4个相同的篮球排成一排，从左到右每个球依次对应的序号为1，2，3，…，8，若同色球之间不加区分，则4个红球对应的序号之和小于4个蓝球对应的序号之和的排列方法种数为31．
其中正确结论的序号为            ．

命题“，”的否定为       ．

下列四个命题：
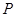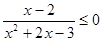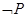① 命题：；则命题是；；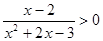
②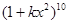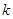（为正整数）的展开式中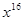，的系数小于90，则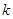的值为1；
③从总体中抽取的样本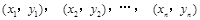.若记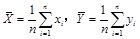，则回归直线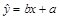必过点 ；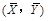
④过双曲线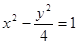的右焦点作直线交双曲线于A、B两点，若弦长|AB|=8，则这样的直线恰好有3条；
其中正确的序号是        （把你认为正确的序号都填上）．

定义向量的运算（其中为向量的夹角），设为非零向量，则下列说法正确的是      ．
①是非负实数
②若向量共线, 则有=0
③若向量垂直，则有=0
④若能构成三角形，则三角形面积

若是两个相交平面，则在下列命题中，真命题的序号为         ．（写出所有真命题的序号）
①若直线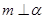，则在平面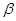内，一定不存在与直线平行的直线．
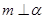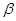②若直线，则在平面内，一定存在无数条直线与直线垂直．
③若直线，则在平面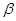内，不一定存在与直线垂直的直线．
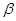④若直线，则在平面内，一定存在与直线垂直的直线．

已知：，：，若是的充分不必要条件，则实数的取值范围是       ．

命题“”的否定为      .

甲、乙、丙三位同学被问到是否去过、、三个城市时，
甲说：我去过的城市比乙多，但没去过城市；
乙说：我没去过城市；
丙说：我们三人去过同一城市；
由此可判断乙去过的城市为.

“p或q”为真命题是“p且q”为真命题的________条件．