[江西]2011—2012学年江西省四校度高二下学期期末联考理科数学试卷
函数 的定义域为( )
的定义域为( )
A. ,1]∪[3,+∞) ,1]∪[3,+∞) |
B. ,1)∪[3,+∞) ,1)∪[3,+∞) |
C. ,1)∪(2,+∞) ,1)∪(2,+∞) |
D. ,1)∪(2,+∞) ,1)∪(2,+∞) |
对四组数据进行统计,获得以下散点图,关于其线性相关系数比较,正确的是( ) 
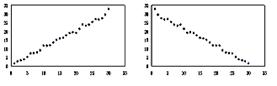
线性相关系数为 线性相关系数为
线性相关系数为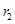 线性相关系数为
线性相关系数为 线性相关系数为
线性相关系数为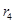
A.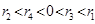 |
B.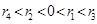 |
C. |
D. |
已知函数f(x)是 上的偶函数,若对于
上的偶函数,若对于 ,都有f(x+2)=f(x),且当
,都有f(x+2)=f(x),且当
x [0,2)时,
[0,2)时, ,则f(-2011)+f(2012) 的值为( )
,则f(-2011)+f(2012) 的值为( )
| A.-2 | B.-1 | C.2 | D.1 |
用数学归纳法证明“ ”对于
”对于 的正整数
的正整数 均成立”时,第一步证明中的起始值
均成立”时,第一步证明中的起始值 应取( )
应取( )
| A. 1 | B. 3 | C. 6 | D.10 |
设 =
= ,则二项式
,则二项式 展开式中不含
展开式中不含 项的系数和是( )
项的系数和是( )
| A.-192 | B.-6 | C.193 | D.7 |
已知 都是定义在
都是定义在 上的函数,并满足:(1)
上的函数,并满足:(1) ;
;
(2) ;(3)
;(3) 且
且 ,则
,则 ( )
( )
A. |
B. |
C. |
D. 或 或 |
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],
都有|f(x)-g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“紧密函数”.若 与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( )
与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( )
| A.[0,1] | B.[2,3] | C.[1,2] | D.[1,3] |
从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球 ,
,
共有 种取法,在这
种取法,在这 种取法中,可以分为两类:一类是取出的m个球全部为白球,
种取法中,可以分为两类:一类是取出的m个球全部为白球,
另一类是取出的m个球中有1个黑球,共有 种取法,
种取法,
即有等式: 成立.试根据上述思想可得
成立.试根据上述思想可得 (用组合数表示)
(用组合数表示)
、对于函数 与函数
与函数 有下列命题:
有下列命题:
①无论函数 的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
②函数 的图像与两坐标轴及其直线
的图像与两坐标轴及其直线 所围成的封闭图形的面积为4;
所围成的封闭图形的面积为4;
③方程 有两个根;
有两个根;
④函数 图像上存在一点处的切线斜率小于0;
图像上存在一点处的切线斜率小于0;
⑤若函数 在点P处的切线平行于函数
在点P处的切线平行于函数 在点Q处的切线,则直线PQ的斜率为
在点Q处的切线,则直线PQ的斜率为 ,其中正确的命题是________.(把所有正确命题的序号都填上)
,其中正确的命题是________.(把所有正确命题的序号都填上)
(本小题满分12分)已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈ 时,函数f(x)=x+> 恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
时,函数f(x)=x+> 恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
(本小题满分12分)已知在直角坐标系xoy中,曲线 的参数方程为
的参数方程为
(t为非零常数, 为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以
为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为 .
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数 ,使得直线
,使得直线 与曲线C有两个不同的公共点
与曲线C有两个不同的公共点 、
、 ,且
,且
(其中o为坐标原点)?若存在,请求出;否则,请说明理由
(本小题满分12分)设二次函数 在区间
在区间 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合 .
.
(Ⅰ)若 ,且
,且 ,求M和m的值;
,求M和m的值;
(Ⅱ)若 ,且
,且 ,记
,记 ,求
,求 的最小值.
的最小值.
(本小题满分12分)在第9届校园文化艺术节棋类比赛项目报名过程中,我校高二(2)班共有16名男生和14名女生预报名参加,调查发现,男、女选手中分别有10人和6人会围棋.
(I)根据以上数据完成以下2 2列联表:
2列联表:
| |
会围棋 |
不会围棋 |
总计 |
| 男 |
|
|
|
| 女 |
|
|
|
| 总计 |
|
|
30 |
并回答能否在犯错的概率不超过0.10的前提下认为性别与会围棋有关?
参考公式: 其中n=a+b+c+d
其中n=a+b+c+d
参考数据:
 |
0.40 |
0.25 |
0.10 |
0.010 |
 |
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若从会围棋的选手中随机抽取3人成立该班围棋代表队,则该代表队中既有男又
有女的概率是多少?
(Ⅲ)若从14名女棋手中随机抽取2人参加棋类比赛,记会围棋的人数为 ,求
,求 的期望.
的期望.
(本小题满分13分)若集合 具有以下性质:①
具有以下性质:① ②若
②若 ,则
,则 ,且
,且 时,
时, .则称集合
.则称集合 是“好集”.
是“好集”.
(Ⅰ)分别判断集合 ,有理数集Q是否是“好集”,并说明理由;
,有理数集Q是否是“好集”,并说明理由;
(Ⅱ)设集合 是“好集”,求证:若
是“好集”,求证:若 ,则
,则 ;
;
(Ⅲ)对任意的一个“好集”A,分别判断下面命题的真假,并说明理由.
命题 :若
:若 ,则必有
,则必有 ;
;
命题 :若
:若 ,且
,且 ,则必有
,则必有 ;
;
 ( )
( ) ,集合
,集合 ,
, ,则
,则 .表示的集合为( )
.表示的集合为( ) 



 ”是“
”是“ ”的充分而不必要条件,则实数
”的充分而不必要条件,则实数 的取值范围是( )
的取值范围是( )



 函数
函数 ,
, 且
且 , 则
, 则 的取值范围是 .
的取值范围是 . 相互独立,若
相互独立,若 ,则
,则 .
. ,设
,设 ,则由函数
,则由函数 的图象与x轴、直线
的图象与x轴、直线 所围成的封闭图形的面积为 .
所围成的封闭图形的面积为 .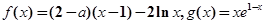 ,(
,(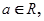 e为自然对数的底数)
e为自然对数的底数)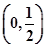 上无零点,求a的最小值;
上无零点,求a的最小值;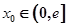 ,在
,在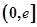 上总存在两个不同的
上总存在两个不同的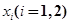 ,使得
,使得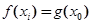 成立,求a的取值范围.
成立,求a的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号