（本小题满分12分）已知在直角坐标系xoy中，曲线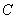
的参数方程为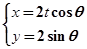
（t为非零常数，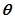
为参数），在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以
轴正半轴为极轴）中，直线
的方程为
．
（Ⅰ）求曲线C的普通方程并说明曲线的形状；
（Ⅱ）是否存在实数
，使得直线与曲线C有两个不同的公共点
、
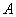，且
（其中o为坐标原点）？若存在，请求出；否则，请说明理由
是等比数列
的前
项和，且
，
．
；
，求数列
的前
．
的最大值.
为锐角，且
.
其中，
的最小正周期及单调减区间.
中，E是AD中点，BE∩AC=F，
，求
的值.
相关知识点
推荐套卷
（本小题满分12分）已知在直角坐标系xoy中，曲线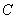的参数方程为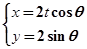
（t为非零常数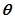，为参数），在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以轴正半轴为极轴）中，直线的方程为．
（Ⅰ）求曲线C的普通方程并说明曲线的形状；
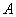（Ⅱ）是否存在实数，使得直线与曲线C有两个不同的公共点、，且
（其中o为坐标原点）？若存在，请求出；否则，请说明理由
粤公网安备 44130202000953号