设命题P:指数函数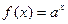 在
在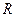 上单调递
上单调递 减,命题Q:不等式
减,命题Q:不等式 对
对 恒成立,如果P或Q为真,P且Q为假,求
恒成立,如果P或Q为真,P且Q为假,求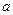 的取值
的取值 范围。
范围。
二.解答题:(计90分)
已知两个命题r(x):sinx+cosx>m;s(x):x2+mx+1>0.如果对于任意实数x,r(x)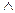 s(x) 为假,r(x)
s(x) 为假,r(x) s(x)为真,求实数m的取值范围。
s(x)为真,求实数m的取值范围。
(本题满分12分)
设p:实数x满足 ,其中
,其中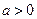 ,命题
,命题 实数
实数 满足
满足 .
.
(Ⅰ)若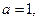 且
且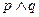 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若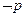 是
是
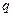 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
设命题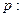 实数
实数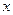 满足
满足 (
(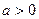 ),命题
),命题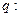 实数
实数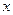 满足
满足 ,
,
(1)若 ,且
,且 为真,求实数
为真,求实数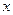 的取值范围;
的取值范围;
(2)若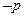 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数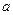 的取值范围。
的取值范围。
已知 p:方程 有两个不等的实根;q:方程
有两个不等的实根;q:方程 无实根.若“p”为假命题,“q”为真命题,求实数 m 的取值范围.
无实根.若“p”为假命题,“q”为真命题,求实数 m 的取值范围.
(本小题满分12分)
写出命题“一组对边平行且相等的四边形是平行四边形”的逆命题,否命题,逆否命题,并且判断其真假.
(本小题满分10分)
设命题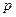 :实数x满足
:实数x满足 ,其中
,其中 ,命题
,命题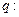 实数
实数 满足
满足 .
.
(Ⅰ)若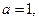 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若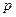 是
是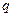 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
(本小题满分12分)
设有两个命题p:关于x的不等式 (a > 0,且a ≠ 1)的解集是{ x |
(a > 0,且a ≠ 1)的解集是{ x |  x < 0 };
x < 0 };
q:函数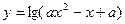 的定义域为R.如果
的定义域为R.如果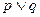 为真命题,
为真命题,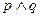 为假命题,
为假命题,
求实数a的取值范围.