高中数学三面角、直三面角的基本性质试题

．（本小题满分13分）汽车和自行车分别从地和地同时开出，如下图，各沿箭头方向（两方向垂直）匀速前进，汽车和自行车的速度分别是10米/秒和5米/秒，已知米.（汽车开到地即停止）

（Ⅰ）经过秒后，汽车到达处，自行车到达处，设间距离为，试
写出关于的函数关系式，并求其定义域.
（Ⅱ）经过多少时间后，汽车和自行车之间的距离最短？最短距离是多少？

设集合为方程的解集，集合为方程的解集，
，求。

设，则（  ）

A．3

B．1

C． 0

D．-1

若函数,,,则由表中数据确定、、依次对应       （    ）.

A．、、	B．、、
C．、、	D．、、

（13分，理科做）已知函数的定义域为，且同时满足：①；②恒成立；③若，则有．
（1）试求函数的最大值和最小值；
（2）试比较与的大小N）；
（3）某人发现：当x=(nÎN)时，有f(x)<2x＋2.由此他提出猜想：对一切xÎ(0,1,都有，请你判断此猜想是否正确，并说明理由．

设函数的定义域为，若存在非零实数满足，均有，且，则称为上的高调函数．如果定义域为的函数是奇函数，当时，，且为上的高调函数，那么实数的取值范围是（   ）

A．

B．

C．

D．

(本题9分)已知函数.
(1) 判断函数的奇偶性； (2) 求该函数的值域；⑶ 利用定义法证明是上的增函数

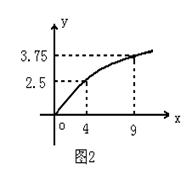
(本题8分)某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2（注：利润与投资单位是万元）
（1）分别将A，B两种产品的利润表示为投资的函数，并写出它们的函数关系式
（2）该企业已筹集到10万元资金，并全部投入A，B两种产品的生产，问：怎样分配这10万元投资，才能是企业获得最大利润，其最大利润约为多少万元（精确到1万元）.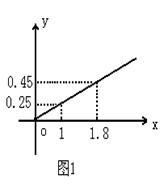

若直角坐标平面内，、两点满足条件：①点、都在函数图像上；②点、关于原点对称，则称点对（、）是函数的一个“姐妹点对”（点对（、）与点（、）可看作同一个“姐妹对”）．
已知函数 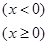 ，则的“姐妹点对”的个数为     （   ）

A．1

B．2

C．3

D．4

若，则 (    )

A．

B．

C．

D．

已知函数f(x)=|2x﹣3|，若0<2<b+1，且，则T=3a²+b的取值范围

A．(，+∞)

B．(，0)

C．(0，)

D．(，0)

某商店同时卖出两套西服，售价均为168元，以成本计算，一套盈利20%，另一套亏损20%，此时商店

A．不亏不盈

B．盈利37.2元

C．盈利14元

D．亏损14元

如图为河岸一段的示意图，一游泳者站在河岸的A点处，欲前往河对岸的C点处。若河宽BC为100m，A、B相距100m，他希望尽快到达C，准备从A步行到E（E为河岸AB上的点），再从E游到C。已知此人步行速度为v，游泳速度为0.5v。
（I）设，试将此人按上述路线从A到C所需时间T表示为的函数；并求自变量 取值范围；
II）当为何值时，此人从A经E游到C所需时间T最小，其最小值是多少？

如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中把草坪分成面积相等的两部分，在上，在上.

（1）设，求用表示的函数关系式；
（2）如果是灌溉水管，为节约成本，希望它最短，的位置应在哪里？如果是参观线路，则希望它最长，的位置又应在哪里？请说明理由.

二次函数中，，则函数的零点个数是（   ）

A．0个

B．1个

C．2个

D．无法确定