已知 是定义在
是定义在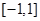 上的奇函数,且
上的奇函数,且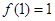 ,若
,若 ,
, 有
有 恒成立.
恒成立.
(1)判断 在
在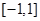 上是增函数还是减函数,并证明你的结论;
上是增函数还是减函数,并证明你的结论;
(2)若 对所有
对所有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
某社区有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动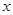 小时的收费为
小时的收费为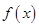 元
元 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动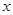 小时的收费为
小时的收费为 元
元 .试求
.试求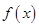 和
和 .
.
(2)问:小张选择哪家比较合算?为什么?
某商场销售某种商品的经验表明,该商品每日的销售量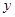 (单位:千克)与销售价格
(单位:千克)与销售价格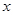 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式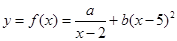 ,其中
,其中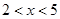 ,
,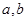 为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
(1)求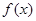 的解析式;
的解析式;
(2)若该商品的成本为2元/千克,试确定销售价格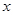 的值,使商场每日销售该商品所获得的利润
的值,使商场每日销售该商品所获得的利润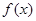 最大.
最大.
已知函数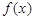 的定义域为
的定义域为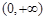 ,若
,若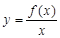 在
在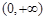 上为增函数,则称
上为增函数,则称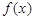 为“一阶比增函数”;若
为“一阶比增函数”;若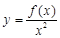 在
在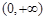 上为增函数,则称
上为增函数,则称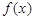 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为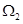 .
.
(Ⅰ)已知函数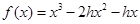 ,若
,若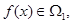 且
且 ,求实数
,求实数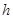 的取值范围;
的取值范围;
(Ⅱ)已知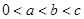 ,
,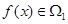 且
且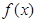 的部分函数值由下表给出,
的部分函数值由下表给出,
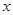 |
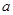 |
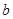 |
 |
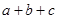 |
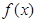 |
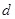 |
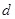 |
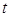 |
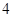 |
求证: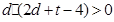 ;
;
(Ⅲ)定义集合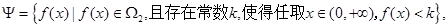
请问:是否存在常数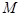 ,使得
,使得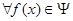 ,
,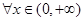 ,有
,有 成立?若存在,求出
成立?若存在,求出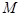 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
对于具有相同定义域 的函数
的函数 和
和 ,若存在
,若存在 ,使得
,使得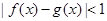 ,则
,则 和
和 在
在 上是“亲密函数”.给出定义域均为
上是“亲密函数”.给出定义域均为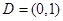 的四组函数如下:
的四组函数如下:
① ②
②
③ 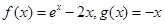 ④
④
其中,函数 和
和 在
在 上是“亲密函数”的是 .
上是“亲密函数”的是 .