高中数学三面角、直三面角的基本性质试题

在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点，如果函数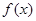的图象恰好通过个整点，则称函数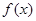为阶整点函数。有下列函数：
；  ②   ③     ④，
其中是一阶整点函数的是(       )

A．①②③④

B．①③④

C．①④

D．④

某学生在复习指数函数的图象时发现：在y轴左边, y=3^x与y=2^x的图象均以x轴负半轴为渐近线, 当x=0时, 两图象交于点（0, 1）．这说明在y轴的左边y=3^x与y=2^x的图象从左到右开始时几乎一样, 后来y=2^x的图象变化加快使得y=2^x与y=3^x的图象逐渐远离, 而当x经过某一值x₀以后 y= 3^x的图象变化加快使得y=2^x与y=3^x的图象又逐渐接近, 直到x=0时两图象交于点（0, 1）．那么x₀=（   ）

A．	B．
C．	D．

若关于的二元一次方程组有唯一一组解，则实数的取值范围是 

设是定义在的可导函数，且不恒为0，记．若对定义域内的每一个，总有，则称为“阶负函数 ”；若对定义域内的每一个，总有，则称为“阶不减函数”（为函数的导函数）．
（1）若既是“1阶负函数”，又是“1阶不减函数”，求实数的取值范围；
（2）对任给的“2阶不减函数”，如果存在常数，使得恒成立，试判断是否为“2阶负函数”？并说明理由．

在下列函数中: ①；②；③；④；⑤其中且；⑥.其中最小值为2的函数是　　　　　　（填入序号 ）.

已知函数是偶函数，直线与函数的图象自左向右依次交于四个不同点，，，．若，则实数的值为     ．

已知函数，.
(1)设函数，求函数的单调区间；
(2)是否存在实数，使得方程在区间内有且只有两个不相等的实数根？若存在，请求出的取值范围；若不存在，请说明理由．

已知为全集，,则（   ）

A．	B．
C．	D．

已知定义在R上的函数满足：对任意x∈R，都有成立，且当时，(其中为的导数).设，则a，b，c三者的大小关系是（   ）

A．

B．

C．

D．

已知函数，设
（1）试确定的取值范围，使得函数在上为单调函数；
（2）求函数在上的最小值．

如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中把草坪分成面积相等的两部分，在上，在上.

（1）设，求用表示的函数关系式；
（2）如果是灌溉水管，为节约成本，希望它最短，的位置应在哪里？如果是参观线路，则希望它最长，的位置又应在哪里？请说明理由.

判断y=1－2x³在上的单调性，并用定义证明.

已知函数（），．
（Ⅰ）若曲线与在它们的交点处具有公共切线，求的值；
（Ⅱ）当时，求函数在区间上的最大值．

已知函数．
(1)求的单调区间；
(2)当时，判断和的大小，并说明理由；
(3)求证：当时，关于的方程：在区间上总有两个不同的解．

设奇函数的定义域为Ｒ，最小正周期，若，则的取值范围是

A．	B．
C．	D．