设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A.y=cos 2x,x∈R |
| B.y=log2|x|,x∈R且x≠0 |
C.y=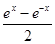 ,x∈R ,x∈R |
| D.y=x3+1,x∈R |
已知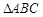 的三内角分别为
的三内角分别为 ,向量
,向量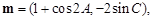
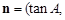
 ,记函数
,记函数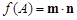 .
.
(1)若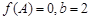 ,求
,求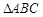 的面积;
的面积;
(2)若关于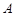 的方程
的方程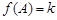 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
已知函数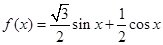 在
在 处取得最大值,则
处取得最大值,则 可能是( )
可能是( )
A. |
B.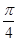 |
C. |
D.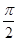 |
设函数 在区间
在区间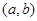 上的导函数为
上的导函数为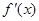 ,
,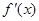 在区间
在区间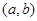 上的导函数为
上的导函数为 ,若在区间
,若在区间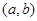 上
上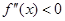 恒成立,则称函数
恒成立,则称函数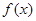 在区间
在区间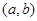 上为“凸函数”.已知
上为“凸函数”.已知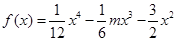 ,若对任意的实数
,若对任意的实数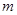 满足
满足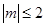 时,函数
时,函数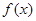 在区间上
在区间上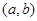 为“凸函数”,则
为“凸函数”,则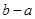 的最大值为( )
的最大值为( )
| A.4 | B.3 | C.2 | D.1 |