设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A.y=cos 2x,x∈R |
| B.y=log2|x|,x∈R且x≠0 |
C.y=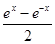 ,x∈R ,x∈R |
| D.y=x3+1,x∈R |
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.有下列函数:
①f(x)=x+ (x>0);②g(x)=x3;
(x>0);②g(x)=x3;
③h(x)=( )x;④φ()=lnx.
)x;④φ()=lnx.
其中是一阶整点函数的是( )
| A.①②③④ | B.①③④ |
| C.④ | D.①④ |
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称函数f(x)为M上的l高调函数.现给出下列命题:
①函数f(x)=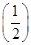 x是R上的1高调函数;
x是R上的1高调函数;
②函数f(x)=sin 2x为R上的π高调函数;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).
其中正确的命题是________.(写出所有正确命题的序号)
已知f(x)=32x-(k+1)3x+2,当x∈R时,f(x)恒为正值,则k的取值范围是( )
| A.(-∞,-1) | B.(-∞,2 -1) -1) |
C.(-1,2 -1) -1) |
D.(-2 -1,2 -1,2 -1) -1) |
定义在 上的偶函数,
上的偶函数,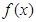 满足
满足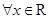 ,都有
,都有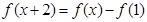 ,且当
,且当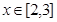 时,
时,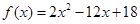 .若函数
.若函数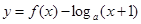 在
在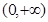 上有三个零点,则
上有三个零点,则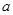 的取值范围是 .
的取值范围是 .
已知函数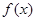 满足
满足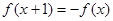 ,且
,且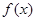 是偶函数,当
是偶函数,当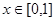 时,
时,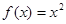 ,若在区间
,若在区间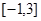 内,函数
内,函数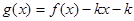 有三个零点,则实数k的取值范围是( )
有三个零点,则实数k的取值范围是( )
A.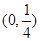 |
B.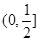 |
C.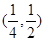 |
D.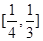 |
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可洗掉蔬菜上残留农药的 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数 .
.
⑴试规定 的值,并解释其实际意义;
的值,并解释其实际意义;
⑵试根据假定写出函数 应满足的条件和具有的性质;
应满足的条件和具有的性质;
⑶设 ,现有
,现有 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.