[山东]2014届山东省烟台市高三上学期期末考试文科数学试卷
已知直线l 平面
平面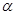 ,直线
,直线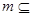 平面
平面 ,则下列四个结论:
,则下列四个结论:
①若 ,则
,则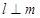 ②若
②若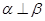 ,则
,则
③若 ,则
,则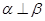 ④若
④若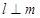 ,则
,则
其中正确的结论的序号是:( )
| A.①④ | B.②④ | C.①③ | D.②③ |
已知函数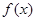 满足
满足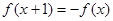 ,且
,且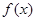 是偶函数,当
是偶函数,当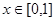 时,
时,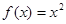 ,若在区间
,若在区间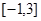 内,函数
内,函数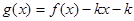 有三个零点,则实数k的取值范围是( )
有三个零点,则实数k的取值范围是( )
A.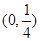 |
B.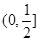 |
C.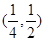 |
D.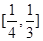 |
若直线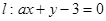 与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以
与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以 为半径的圆与直线l相切,则△AOB面积为_____________.
为半径的圆与直线l相切,则△AOB面积为_____________.
给出以下四个结论:
①函数 的对称中心是
的对称中心是
②若不等式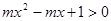 对任意的x∈R都成立,则
对任意的x∈R都成立,则 ;
;
③已知点 与点Q(l,0)在直线
与点Q(l,0)在直线 两侧,则
两侧,则 ;
;
④若将函数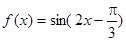 的图像向右平移
的图像向右平移 个单位后变为偶函数,则
个单位后变为偶函数,则 的最小值是
的最小值是 .
.
其中正确的结论是____________(写出所有正确结论的编号).
在平面直角坐标系中,角α,β的始边为x轴的非负半轴,点 在角α的终边上,点
在角α的终边上,点 在角β的终边上,且
在角β的终边上,且
(1)求
(2)求P,Q的坐标并求 的值
的值
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形, ,
, ,DC=1,AB=2,PA⊥平面ABCD,PA=1.
,DC=1,AB=2,PA⊥平面ABCD,PA=1.
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录。为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足 (其中
(其中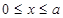 ,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为
,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为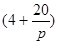 万元/万件.
万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润是大?
已知 是二次函数,不等式
是二次函数,不等式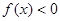 的解集是
的解集是 ,且
,且 在点
在点 处的切线与直线
处的切线与直线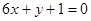 平行.
平行.
(1)求 的解析式;
的解析式;
(2)是否存在t∈N*,使得方程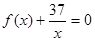 在区间
在区间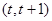 内有两个不等的实数根?
内有两个不等的实数根?
若存在,求出t的值;若不存在,说明理由.
 ,集合
,集合 ,
, ,则
,则
 等于( )
等于( )



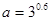 ,
,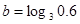 ,
, ,则( )
,则( )



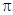 ,且图象关于直线
,且图象关于直线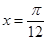 对称的是( )
对称的是( )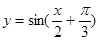
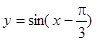

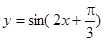
 ,
, ,若
,若 ,则
,则 等于( )
等于( )

 ABC中,若
ABC中,若 ,则A=( )
,则A=( )



 的零点所在的区间是( )
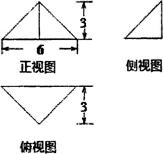
的零点所在的区间是( ) 的图象的大致形状是( )
的图象的大致形状是( )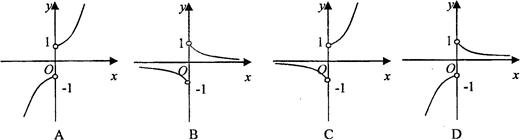
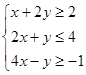 ,则
,则 的取值范围是( )
的取值范围是( )
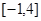
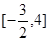

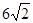

 的渐近线与抛物线
的渐近线与抛物线 相切,则此双曲线的离心率等于( )
相切,则此双曲线的离心率等于( )
 的定义域为______________.
的定义域为______________. 的前n项和为Sn,
的前n项和为Sn, ,则正整数m的值为_____________.
,则正整数m的值为_____________. 的前n项和为
的前n项和为
 ,
,
 为等差数列;
为等差数列; 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn. 的左、右焦点分别为
的左、右焦点分别为 ,且
,且 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点. 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点 ,当
,当 时,求实数m的取值范围,
时,求实数m的取值范围, 粤公网安备 44130202000953号
粤公网安备 44130202000953号