(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数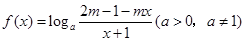 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
(1)求实数m的值,并写出区间D;
(2)若底数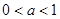 ,试判断函数
,试判断函数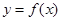 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明;
(3)当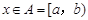 (
(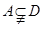 ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数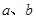 的值.
的值.
已知函数 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的 ,都有f(x)
,都有f(x) 成立,求函数g(t)
成立,求函数g(t) 的最值
的最值
本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图1,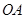 ,
,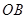 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段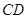 和曲线段
和曲线段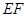 分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥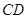 上某点
上某点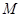 分别修建与
分别修建与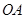 ,
,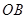 平行的栈桥
平行的栈桥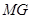 、
、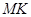 ,且以
,且以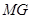 、
、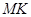 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台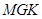 。建立如图2所示的直角坐标系,测得线段
。建立如图2所示的直角坐标系,测得线段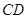 的方程是
的方程是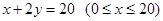 ,曲线段
,曲线段 的方程是
的方程是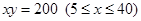 ,设点
,设点 的坐标为
的坐标为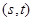 ,记
,记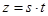 。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
(1)求 的取值范围;
的取值范围;
(2)试写出三角形观光平台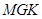 面积
面积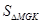 关于
关于 的函数解析式,并求出该面积的最小值
的函数解析式,并求出该面积的最小值
已知a=20.2,b=0.40.2,c=0.40.6,则
| A.a>b>c | B.a>c>b | C.c>a>b | D.b>c> a |
(本题满分18分,第1小题满分5分,第2小题满分5分,第3小题满分8分)
已知函数 ,其中
,其中 .
.
(1)当 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域;
(2)当 ,
, 时,求
时,求 的最小值;
的最小值;
(3)设 ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
直线y=ex+b(e为自然对数的底数)与两个函数 的图象至多有一个公共点,则实数b的取值范围是__________.
的图象至多有一个公共点,则实数b的取值范围是__________.
(本小题满分12分)某投资商到一开发区投资72万元建起了一座蔬菜加工厂,经营中,第一年支出12万元,以后每年支出 增加4万元,从第一年起每年蔬菜销售收入50万元.设
增加4万元,从第一年起每年蔬菜销售收入50万元.设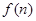 表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元).
表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元). (I)该厂从第几年开始盈利?
(I)该厂从第几年开始盈利?
(II)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
(文科)已知关于x的一元二次方程 。
。
(Ⅰ)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 两个数中任取的一个数,求上述方程有实根的概率;
两个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率。
任取的一个数,求上述方程有实根的概率。
.已知当x∈R时,函数y=f(x)满足f(2.1+x)="f(1.1+x)" +  ,且f(1)=1,则f(100)的值为( )
,且f(1)=1,则f(100)的值为( )
A. |
B. |
C.34 | D. |
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上, 在
在 上.
上.
(1)设 ,求用
,求用 表示
表示 的函数关系式;
的函数关系式;
(2)如果 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, 的位置应在哪里?如果
的位置应在哪里?如果 是参观线路,则希望它最长,
是参观线路,则希望它最长, 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.