高中数学多面角及多面角的性质解答题

（本题共13分，第Ⅰ问6分，第Ⅱ问7分）
已知函数．
（Ⅰ）求的最小正周期；
（Ⅱ）求的单调递增区间，并求出在上的最大值与最小值．

函数的部分图象如图所示.

（1）写出的最小正周期及图中、的值；
（2）求在区间上的最大值和最小值.

已知函数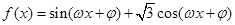（为奇函数,且函数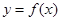的图象的两相邻对称轴之间的距离为.
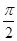（Ⅰ）求的值;
（Ⅱ）将函数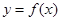的图象向右平移个单位后,得到函数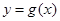的图象,求函数的单调递增区间.

（本小题满分12分）设向量.
（1）若向量，求的值；
（2）设函数的最大值.

（本小题满分12分）设函数
（1）求的最大值，并写出使取最大值时的集合；
（2）已知中，角的对边分别为若，求的最小值。

已知函数（， ，求函数的最小值。

已知，且
（1）求实数m的值。
（2）求的单调区间。

设函数．
（1）求函数的最小正周期和单调递增区间；
（2）当时，的最大值为2，求的值，并求出的对称轴方程．

（本小题满分13分）已知函数.
（1）求的值；
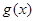（2）求的单调递增区间.

已知函数，
（1）求函数的对称轴所在直线的方程；
（2）求函数单调递增区间．

已知函数=（A>0,）的图像如图所示.

（1）求，，；
（2）求的单调增区间并说明如何由=变换得到y=的图像.

已知函数为常数）
（1）若，求的单调区间;
（2）当时,设的最大值为,最小值,若,求的值．

已知向量a＝（cosx，－），b＝（sinx，cos2x），x∈R，设函数f（x）＝a·b．
（1）求f（x）的最小正周期；
（2）求f（x）在[0，]上的最大值和最小值．

已知函数，其图象过点（,）．
（1）求的值；
（2）将函数的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数的图象，求函数在[0, ]上的最大值和最小值．

设．
（1）求的最大值及最小值周期；
（2）在中，角的对边分别为，锐角满足，求的值