高中数学多面角及多面角的性质解答题

函数在一个周期内，当 时， 取得最小值 ；当 时， 取得最大值4，试求 的函数表达式.

保持正弦曲线上所有点的纵坐标不变，横坐标缩短为原来的，再将图像沿 轴向右平移 个单位，得到函数 的图像.
（1）写出的表达式，并计算.
（2）求出在 上的值域.

已知函数
（1）求函数的最小正周期和单调递减区间；
（2）在中，分别是角A、B、C的对边，若,求 面积的最大值．

已知函数图象的一部分如图所示．
（1）求函数的解析式；
（2）当时，求函数的最大值与最小值及相应的的值．

设函数，图象的一条对称轴是直线.
（1）求；      
（2）求函数的单调增区间；
（3）画出函数在区间[0，π]上的图象．

已知
（1）求函数的最小正周期及在区间上的最大值和最小值；
（2）若，，求的值.

已知A(x₁,f(x₁))，B(x₂,f(x₂))是函数f(x)=2sin(wx+j)(w＞0,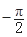＜j＜0)图象上的任意两点，且角j的终边经过点P(l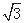，-)，若|f(x₁)-f(x₂)|=4时，|x₁-x₂|的最小值为.
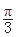(1)求函数f(x)的解析式；(2)求函数f(x)的单调递增区间；(3)当x∈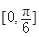时，不等式mf(x)+2m≥f(x)恒成立，求实数m的取值范围.

已知函数.
（1）求的单调递增区间；
（2）若是第二象限角，，求的值.

已知函数，.
（1）求的最小正周期；
（2）求在闭区间上的最大值和最小值.

已知函数.
（1）把的解析式Acos()+B的形式，并用五点法作出在一个周期上的简图;(要求列表)
（2）说出的图像经过怎样的变换的图像.

已知函数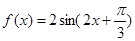
（1）求函数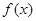的最小正周期及单调递减区间；
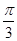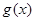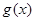（2）若将函数的图像向右平移个单位，得到函数的图像，求在区间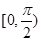上的最大值和最小值，并求出相应的x的取值。

已知函数图象的一部分如图所示．
（1）求函数的解析式；
（2）当时，求函数的最大值与最小值及相应的的值．

已知函数f(x)＝ (sin²x－cos²x)－2sinxcosx.
(1)求f(x)的最小正周期；
(2)设x∈[－，]，求f(x)的值域和单调递增区间．

设函数.
（1）求的最小正周期；
（2）若函数的图像向右、向上分别平移个单位长度得到的图像，求在的最大值.

设函数f (x)＝cos(2x＋)＋sin2x＋2a
（1）求函数f (x)的单调递增区间
（2）当0≤x≤时，f (x)的最小值为0，求a的值．