高中数学多面角及多面角的性质解答题

已知向量，，且的最小正周期为
（Ⅰ）求的值；
（Ⅱ）若，解方程；
（Ⅲ）在中，，,且为锐角，求实数的取值范围.

如图,已知OPQ是半径为1，圆心角为的扇形，C是扇形弧上的动点,ABCD是扇形的内接矩形,记,求当角取何值时, 矩形ABCD的面积最大?并求出这个最大值.

设，
（1）写出函数的最小正周期及单调增区间；
（2）若时，求函数的最值。

设关于的函数的最小值为，试确定满足的的值，并对此时的值求的最大值。

已知函数（Ⅰ）求函数的最小正周期；（Ⅱ）求函数在区间上的最大值和最小值.

已知，．
（1）若，求的单调的递减区间；
（2）若，求的值．

已知函数.
（1）求函数的最小正周期及单调递增区间；
（2）若，求的值.

化简：
（1）
（2）

设函数为最小正周期.
（1）求的解析式；
（2）已知的值.

已知函数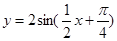 
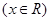
（1）利用“五点法”画出该函数在长度为一个周期上的简图;
列表；

 
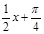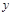作图：

（2）说明该函数的图像可由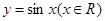的图像经过怎样的变换得到.

已知函数
（1）求函数内的单调递增区间；
（2）求函数内的值域.

已知函数．
（1）求函数的最小值和最小正周期；
（2）已知内角的对边分别为，且，，求的值．

函数 ()的部分图像如右所示.

（1）求函数的解析式；
（2）设，且，求的值.

已知向量a= b=。
（1）求及|a+ b|；
（2）若-|a+b|，求的最大值和最小值。

已知函数，记的内角的对边长分别为，若，求的值。