高中数学多面角及多面角的性质解答题

已知函数的图象过点.
（1）求实数的值； 
（2）求函数的最小正周期及最大值.

已知函数，其定义域为，最大值为6.
（1）求常数m的值；
（2）求函数的单调递增区间.

已知函数.
（1）求的定义域及最小正周期；
（2）求单调递减区间.

设函数f(x)=sin²ωx+2sinωx·cosωx-cos²ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(,0),求函数f(x)的值域.

已知函数f(x)＝Asin，x∈R，A>0，0<φ<，y＝f(x)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(1，A)．

(1)求f(x)的最小正周期及φ的值；
(2)若点R的坐标为(1，0)，∠PRQ＝，求A的值．

已知函数f(x)＝sincos＋cos²－
(1)若f(α)＝，α∈(0，π)，求α的值；
(2)求函数f(x)在上最大值和最小值．

已知函数f(x)＝2sin.
(1)求函数y＝f(x)的最小正周期及单调递增区间；
(2)若f＝－，求f(x₀)的值．

已知f(x)＝cos(ωx＋φ)的最小正周期为π，且f＝.
(1)求ω和φ的值；
(2)在给定坐标系中作出函数f(x)在[0，π]上的图象；

(3)若f(x)>，求x的取值范围．

已知函数的部分图像如图所示.

（1）求的值；
（2）求函数的单调递增区间.

函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.

(1)求f(x)的最小正周期及解析式.
(2)设g(x)=f(x)-cos2x,求函数g(x)在区间[0,]上的最大值和最小值.

已知函数.
（1）当时，求函数的单调递增区间；
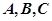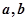（2）设的内角的对应边分别为，且若向量与向量共线，求的值.

已知函数． 的部分图象如图所示，其中点是图象的一个最高点.

（1）求函数的解析式；
（2）已知且，求．

已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<)的图象的一部分如图所示．

(1)求函数f(x)的解析式；
(2)当x∈时，求函数y＝f(x)＋f(x＋2)的最大值与最小值及相应的x的值．

设函数f(x)＝Asin(ωx＋φ)(其中A＞0，ω＞0，－π＜φ≤π)在x＝处取得最大值2，其图象与x轴的相邻两个交点的距离为.
(1)求f(x)的解析式；
(2)求函数g(x)＝的值域．

已知函数f(x)＝sin²x＋sin xcos x，x∈.
(1)求f(x) 的零点；
(2)求f(x)的最大值和最小值．