福建省福州市高三毕业班质检理科数学试卷
“实数 ”是“复数
”是“复数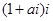 (
( 为虚数单位)的模为
为虚数单位)的模为 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不是充分条件又不是必要条件 |
来源:2014届福建省福州市高三毕业班质检理科数学试卷
已知 、
、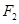 是双曲线
是双曲线 的左、右焦点,若双曲线左支上存在一点一点
的左、右焦点,若双曲线左支上存在一点一点 与点
与点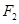 关于直线
关于直线 对称,则该双曲线的离心率为( )
对称,则该双曲线的离心率为( )
A. |
B. |
C. |
D. |
来源:2014届福建省福州市高三毕业班质检理科数学试卷
若定义在R上的函数f(x)满足f(-x)="f(x)," f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间[-3,1]上的零点个数为 ( )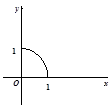

| A.5 | B.4 | C.3 | D.2 |
来源:2014届福建省福州市高三毕业班质检理科数学试卷
在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
规定:当产品中的此种元素含量 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数 的分布列及数学期望
的分布列及数学期望 .
.
来源:2014届福建省福州市高三毕业班质检理科数学试卷
已知函数 .
.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)设 的内角
的内角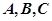 的对应边分别为
的对应边分别为 ,且
,且 若向量
若向量 与向量
与向量 共线,求
共线,求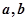 的值.
的值.
来源:2014届福建省福州市高三毕业班质检理科数学试卷
如图,直角梯形 中,
中, ,点
,点 分别是
分别是 的中点,点
的中点,点 在
在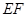 上,沿
上,沿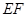 将梯形
将梯形 翻折,使平面
翻折,使平面
 平面
平面 .
.
(1)当 最小时,求证:
最小时,求证: ;
;
(2)当 时,求二面角
时,求二面角 平面角的余弦值.
平面角的余弦值.
来源:2014届福建省福州市高三毕业班质检理科数学试卷
已知动圆 过定点(1,0),且与直线
过定点(1,0),且与直线 相切.
相切.
(1)求动圆圆心 的轨迹方程;
的轨迹方程;
(2)设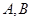 是轨迹
是轨迹 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线 和
和 的倾斜角分别为
的倾斜角分别为 和
和 ,①当
,①当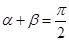 时,求证直线
时,求证直线 恒过一定点
恒过一定点 ;
;
②若 为定值
为定值 ,直线
,直线 是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
来源:2014届福建省福州市高三毕业班质检理科数学试卷
已知矩阵
 ,若矩阵
,若矩阵 属于特征值6的一个特征向量为
属于特征值6的一个特征向量为 ,属于特征值1的一个特征向量
,属于特征值1的一个特征向量 .
.
(1)求矩阵 的逆矩阵;
的逆矩阵;
(2)计算
来源:2014届福建省福州市高三毕业班质检理科数学试卷
在平面直角坐标系 中,以
中,以 为极点,
为极点,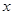 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数),两曲线相交于
为参数),两曲线相交于 两点.
两点.
(1)写出曲线 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(2)若 求
求 的值.
的值.
来源:2014届福建省福州市高三毕业班质检理科数学试卷
 ,若
,若 ,则是实数
,则是实数 的取值范围是( )
的取值范围是( )



 值是( )
值是( )



 ,使得
,使得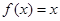 ”的否定是( )
”的否定是( ) ,都有
,都有 ,使
,使
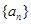 的前
的前 项积记为
项积记为 ,若
,若 ,则
,则 ( )
( ) ,若
,若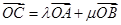 ,且
,且 ,则用阴影表示
,则用阴影表示 点所有可能的位置区域正确的是 ( )
点所有可能的位置区域正确的是 ( )
 的部分图像如图所示,则
的部分图像如图所示,则



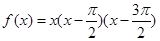
 (
( 、
、 、
、 为常数),当
为常数),当 时取极大值,当
时取极大值,当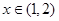 时取极小值,则
时取极小值,则 的取值范围是( )
的取值范围是( )

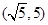


 中任取一点
中任取一点 ,则点
,则点
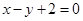 与圆C:
与圆C: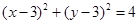 相交于A、B两点,则
相交于A、B两点,则 的值为_______.
的值为_______.
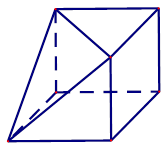
 ,若数列
,若数列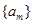 满足
满足 ,且
,且 项和为
项和为 ,则
,则 _____________.
_____________. ,
, 的最小值
的最小值 ;
; 时,求
时,求 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号