2014年高考数学（理）二轮复习专题提升训练优化重组卷2练习卷

已知α∈，cos α＝－，tan 2α等于(　　)．

A．

B．－

C．－2

D．2

已知向量a＝(2,1)，a·b＝10，|a＋b|＝5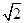，则|b|等于(　　)．

A．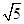

B．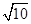

C．5

D．25

将函数y＝cos 2x的图象向右平移个单位，得到函数y＝f(x)·sin x的图象，则f(x)的表达式可以是(　　)．

A．f(x)＝－2cos x	B．f(x)＝2cos x
C．f(x)＝sin 2x	D．f(x)＝(sin 2x＋cos 2x)

已知向量a，b满足|a|＝2，|b|＝1，且(a＋b)⊥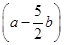，则a与b的夹角为(　　)．

A．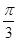

B．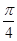

C．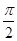

D．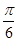

若M为△ABC所在平面内一点，且满足(－)·(＋－2 )＝0，则△ABC为(　　)．

在△ABC中，AB＝2，AC＝3，BC＝4，则角A，B，C中最大角的余弦值为(　　)．

A．－

B．－

C．

D．

已知函数y＝Asin(ωx＋φ)＋m(A>0，|φ|<)的最大值为4，最小值为0，两个对称轴间的最短距离为，直线x＝是其图象的一条对称轴，则符合条件的解析式是(　　)．

A．y＝4sin	B．y＝－2sin＋2
C．y＝－2sin＋2	D．y＝2sin＋2

已知f(x)＝sin x，x∈R，g(x)的图象与f(x)的图象关于点对称，则在区间[0,2π]上满足f(x)≤g(x)的x的范围是(　　)．

A．

B．

C．

D．

已知sin x＝，x∈，则tan＝______.

已知A(1,2)，B(3,4)，C(－2,2)，D(－3,5)，则向量在向量上的投影为______．

在△ABC中，若AB＝1，AC＝|＋|＝||，则＝______.

已知函数f(x)＝sin²x＋sin xcos x，x∈.
(1)求f(x) 的零点；
(2)求f(x)的最大值和最小值．

已知函数f(x)＝Msin(ωx＋φ)(M>0，ω>0，|φ|<)的部分图象如图所示．
 
(1)求函数f(x)的解析式；
(2)在△ABC中，角A，B，C的对边分别是a，b，c，若(2a－c)cos B＝bcos C，求f的取值范围．

在△ABC中，角A，B，C对应的边分别是a，b，c.已知cos 2A－3cos(B＋C)＝1.
(1)求角A的大小；
(2)若△ABC的面积S＝5，b＝5，求sin Bsin C的值．

在△ABC中，角A，B，C所对的边分别为a，b，c，已知cos C＋(cos A－sin A)cos B＝0.
(1)求角B的大小；
(2)若a＋c＝1，求b的取值范围．

已知向量a＝(Asin ωx，Acos ωx)，b＝(cos θ，sin θ)，f(x)＝a·b＋1，其中A>0，ω>0，θ为锐角．f(x)的图象的两个相邻对称中心的距离为，且当x＝时，f(x)取得最大值3.
(1)求f(x)的解析式；
(2)将f(x)的图象先向下平移1个单位，再向左平移φ(φ>0)个单位得g(x)的图象，若g(x)为奇函数，求φ的最小值．