(本小题满分13分)某同学用“五点法”画函数 在某一个周期的图象时,列表并填入的部分数据如下表:
在某一个周期的图象时,列表并填入的部分数据如下表:
(1)求 ,
, ,
, 的值及函数
的值及函数 的表达式;
的表达式;
(2)将函数 的图象向左平移
的图象向左平移 个单位,可得到函数
个单位,可得到函数 的图象,求函数
的图象,求函数 在区间
在区间 的最小值.
的最小值.
(本小题共13分)已知函数 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 在区间
在区间 上的最大值与最小值.
上的最大值与最小值.
已知函数 ,
, .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的最大值和最小值及相应的x的值.
上的最大值和最小值及相应的x的值.
(本小题满分13分)已知函数 .
.
(1)求函数 的最小正周期和函数
的最小正周期和函数 的单调递增区间;
的单调递增区间;
(2)在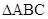 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 ,
, ,
,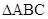 的面积为
的面积为 ,求边长
,求边长 的值.
的值.
(本小题满分12分)
函数 部分图象如图所示.
部分图象如图所示.
(Ⅰ)求 的最小正周期及解析式;
的最小正周期及解析式;
(Ⅱ)设 ,求函数
,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知函数 的一部分图像如右图所示,(其中
的一部分图像如右图所示,(其中 ,
, ,
, ).
).
(Ⅰ)求函数 的解析式并求函数的单调递增区间;
的解析式并求函数的单调递增区间;
(Ⅱ)在 中,角
中,角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, ,若
,若 ,
, ,
, 的面
的面
积为 ,求边长
,求边长 的值.
的值.
(本小题满分12分)
已知函数
 R
R ,
, 是函数
是函数 的一个零点.
的一个零点.
(1)求 的值,并求函数
的值,并求函数 的单调递增区间;
的单调递增区间;
(2)若
 ,且
,且 ,
, ,求
,求 的值.
的值.
已知函数 ,且周期为
,且周期为 .
.
(1)求 的值;
的值;
(2)当 [
[ ]时,求
]时,求 的最大值及取得最大值时
的最大值及取得最大值时 的值.
的值.
(本小题满分12分)已知函数 ,
, (其中
(其中 ),其部分图像如图所示.
),其部分图像如图所示.
(1)求函数 的解析式;
的解析式;
(2)已知横坐标分别为 、
、 、
、 的三点
的三点 都在函数
都在函数 的图像上,求
的图像上,求 的值.
的值.
已知函数 满足
满足
(1)求实数 的值以及函数
的值以及函数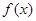 的最小正周期;
的最小正周期;
(2)记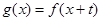 ,若函数
,若函数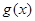 是偶函数,求实数
是偶函数,求实数 的值.
的值.