福建省漳州市普通高中毕业班质量检查理科数学试卷
“ ,
, 且
且 ”是“数列
”是“数列 为等比数列”的( )
为等比数列”的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , ,且 ,且 ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
已知抛物线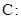
 (
( )的焦点
)的焦点 到双曲线
到双曲线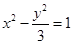 的渐近线的距离为
的渐近线的距离为 ,过焦点
,过焦点 斜率为
斜率为 的直线与抛物线
的直线与抛物线 交于
交于 、
、 两点,且
两点,且 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知函数 定义域
定义域 ,满足
,满足 ,当
,当 时,
时, ,若函数
,若函数 ,方程
,方程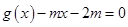 有三个实根,则实数
有三个实根,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在平面直角坐标系 中,设
中,设 是由不等式组
是由不等式组 表示的区域,
表示的区域, 是到原点的距离不大于
是到原点的距离不大于 的点构成的区域,向
的点构成的区域,向 中随机投一点,则所投点落在
中随机投一点,则所投点落在 中的概率是 .
中的概率是 .
(本小题满分13分)已知函数 .
.
(1)求函数 的最小正周期和函数
的最小正周期和函数 的单调递增区间;
的单调递增区间;
(2)在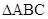 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 ,
, ,
,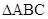 的面积为
的面积为 ,求边长
,求边长 的值.
的值.
(本小题满分13分)根据新修订的《环境空气质量标准》指出空气质量指数在 ,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为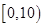 ,
, ,
,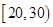 ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1)求 的值;
的值;
(2)根据样本数据,试估计这一年度的空气质量指数的平均值;
(3)用这50个样本数据来估计全年的总体数据,将频率视为概率.如果空气质量指数不超过20,就认定空气质量为“最优等级”.从这一年的监测数据中随机抽取2天的数值,其中达到“最优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)如图1,在 中,
中, ,
, ,
, ,
,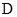 、
、 分别为
分别为 、
、 的中点,连接
的中点,连接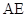 并延长交
并延长交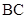 于
于 ,将
,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,如图2所示.
,如图2所示.
(1)求证: 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在线段 上是否存在点
上是否存在点 使得
使得 平面
平面 ?若存在,请指出点
?若存在,请指出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(本小题满分13分)已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 过点
过点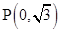 ,离心率
,离心率 .
.
(1)求椭圆 的方程;
的方程;
(2)如图,动直线
 与椭圆
与椭圆 有且仅有一个公共点,
有且仅有一个公共点, 求
求 ,
, 满足的关系式;
满足的关系式; 如图,
如图, 、
、 为椭圆
为椭圆 的左、右焦点,作
的左、右焦点,作 ,
,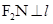 ,垂足分别为
,垂足分别为 、
、 ,四边形
,四边形 的面积
的面积 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
(本小题满分14分)已知函数 (
( ).
).
(1)若 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;
(2)若 ,
, 已知
已知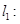
 ,
,
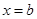 ,若直线
,若直线 、
、 及直线
及直线 与函数
与函数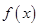 的图象所围成的封闭图形如阴影部分所示,求阴影面积
的图象所围成的封闭图形如阴影部分所示,求阴影面积 关于
关于 的函数
的函数 的最小值
的最小值 ;
; 证明不等式:
证明不等式: .
.
(本小题满分7分)选修4-2:矩阵与变换
已知矩阵 .
.
(1)矩阵 对应的变换把直线
对应的变换把直线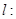
 变为直线
变为直线 ,求直线
,求直线 的方程;
的方程;
(2)求 的逆矩阵
的逆矩阵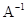 .
.
(本小题满分7分)选修4-4:坐标系与参数方程
已知直线 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: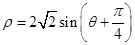 .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)判断直线 与圆
与圆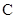 的位置关系.
的位置关系.
 ,集合
,集合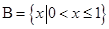 ,则集合
,则集合 ( )
( )




 ,
, ,则( )
,则( )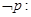
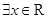 ,
,




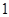

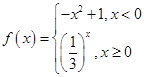 的图象大致为( )
的图象大致为( )
 的展开式中常数项为( )
的展开式中常数项为( )



 ,则判断框内应填( )
,则判断框内应填( )




 ,
, ,向量
,向量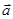 与
与 的夹角为
的夹角为 ,则
,则 .
. 为纯虚数,若
为纯虚数,若 (
( 为虚数单位),则实数
为虚数单位),则实数 的值为 .
的值为 .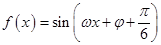 (
( ,
, )的部分图象如图所示,则
)的部分图象如图所示,则 的值为 .
的值为 .
 (
( ,
, ),若数列
),若数列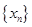 是等差数列,记集合
是等差数列,记集合 的元素个数为
的元素个数为 ,则
,则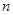 的表达式为 .
的表达式为 .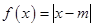 .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值; ,
, ,
, 满足
满足 ,求
,求 的最大值.
的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号