已知函数 .
.
(Ⅰ)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(Ⅱ)在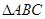 中,角
中,角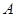 ,
,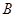 ,
, 的对边分别是
的对边分别是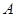 ,
,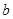 ,
, ;若
;若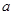 ,
,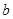 ,
, 成等比数列,且
成等比数列,且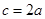 ,
,
求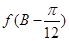 的值.
的值.
设 在
在 上的最大值为3
上的最大值为3
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,
, ,求
,求 及
及 的面积.
的面积.
(本小题满分12分)已知函数 .
.
(1)求 的值;
的值;
(2)求函数 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(3)说明 的图像是如何由函数
的图像是如何由函数 的图像变换所得.
的图像变换所得.
(本小题满分12分)已知函数 的图象与直线
的图象与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为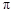 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)设 的内角
的内角 所对的边分别是
所对的边分别是 .若
.若
 ,求角
,求角 的大小.
的大小.
【改编】【2014年广东省东莞市高三第二次模拟理】已知函数 .
.
(1)求函数 的图象的对称中心;
的图象的对称中心;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知 ,b,a,c成等差数列,且
,b,a,c成等差数列,且 ,求a的值.
,求a的值.
【改编】(本小题满分12分)已知函数 .
.
(1)求 及函数
及函数 的最小正周期;
的最小正周期;
(2)当 时,求函数
时,求函数 的最值
的最值
【改编】已知函数 .
.
(1)若 ,求
,求 的值域;
的值域;
(2)在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,且
,且 ,求边
,求边 的长.
的长.
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ)若函数 的图象关于直线
的图象关于直线 对称,求
对称,求 的最小值;
的最小值;
(Ⅱ)若函数 在
在 上有零点,求实数
上有零点,求实数 的取值范围.
的取值范围.
(本小题满分12分)设函数 的图象的最高点D的坐标为(2,
的图象的最高点D的坐标为(2, ),由最高点运动到相邻的最低点F时,曲线与x轴相交于点E(6,0).
),由最高点运动到相邻的最低点F时,曲线与x轴相交于点E(6,0).
(1)求 的值;
的值;
(2)求函数 ,使其图象与
,使其图象与 图象关于直线
图象关于直线 对称.
对称.
(本小题满分12分)若函数
 的图象与直线
的图象与直线 相切,
相切,
并且相邻两个切点的距离为 .
.
(1)求 ,
, 的值;
的值;
(2)将 的图象向右平移
的图象向右平移 个单位后,所得的图象
个单位后,所得的图象 对应的函数
对应的函数 恰好是偶函数,求最
恰好是偶函数,求最
小正数 ,并求
,并求 的单调递增区间。
的单调递增区间。
(本小题满分12分)已知函数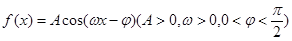 的周期为π,且图象上一个最低点为M(
的周期为π,且图象上一个最低点为M(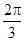 ,-2).
,-2).
(1)求f(x)的解析式;(2)当x∈[0,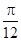 ]时,求f(x)的值域.
]时,求f(x)的值域.
(本小题满分12分)已知函数 (其中A、B、
(其中A、B、 是实数,且
是实数,且 )的最小正周期为
)的最小正周期为 ,并且当
,并且当 时,
时, 取得最大值
取得最大值 。
。
(1)求函数 的表达式;
的表达式;
(2)在闭区间 是否存在
是否存在 的对称轴?如果存在,求其对称轴方程;若不存在,说明理由。
的对称轴?如果存在,求其对称轴方程;若不存在,说明理由。