高中数学多面角及多面角的性质解答题

（本题12分）已知角终边上一点的坐标为，
（1）求角的集合．
（2）化简下列式子并求其值：；

（本题12分）已知求的值。

已知函数。
（1）求的振幅和最小正周期；
（2）求当时,函数的值域；
（3）当时，求的单调递减区间。

已知
（Ⅰ）求函数图象的对称中心的横坐标；
（Ⅱ）若，求函数的值域。

已知函数，求：
（1）求函数的最小正周期；
（2）求函数的最大值、最小值及取得最大值、最小值的
（3）求函数的单调递增区间

(10分)已知函数 
（１）求的最小正周期和值域     （２）求的单调递增区间

在中，角所对的边分别为且满足
（I）求角的大小；
（II）求函数 的最大值，并求取得最大值时的大小．

本题满分12分）已知函数的一条对称轴为，且
（1）求f(x)的解析式；（2）求f(x)的最小正周期、单调增区间及对称中心。

（本小题满分12分）
已知函数其中，
（I）若求的值；         
（Ⅱ）在（I）的条件下，若函数的图像的相邻两条对称轴之间的距离等于，
①      求函数的解析式；②求最小正实数，使得函数的图象向左平移个单位时对应的函数是偶函数.

已知函数，
（1）用五点法画出它在一个周期内的闭区间上的图象；
（2）求单调增减区间。

已知为第三象限角，.
（1）化简；
（2）若，求的值.

(本小题满分13分)函数的部分图象如下图所示，该图象与轴交于点，与轴交于点，为最高点，且的面积为．

（Ⅰ）求函数的解析式；
（Ⅱ），求的值．
（Ⅲ）将函数的图象的所有点的横坐标缩短到原来的倍（纵坐标不变），再向左平移个单位，得函数的图象，若函数为奇函数，求的最小值.

如图,有一块边长为1（百米）的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角始终为（其中点P，Q分别在边BC，CD上）,设．

（Ⅰ）用t表示出PQ的长度,并探求的周长l是否为定值；
（Ⅱ）问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少（平方百米）?

（本小题满分12分）
已知平面直角坐标系中，，，，．
（Ⅰ）求的最小正周期和对称中心；
（Ⅱ）求在区间上的单调递增区间．

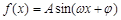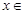已知函数(R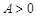，，，)图象如图，P是图象的最高点，Q为图象与轴的交点，O为原点．且，，．

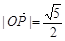（Ⅰ）求函数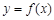的解析式；
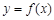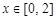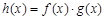（Ⅱ）将函数图象向右平移1个单位后得到函数的图象，当时，求函数的最大值．