(本小题满分12分)函数 的图象上相邻的最高点与最低点的坐标分别为M(
的图象上相邻的最高点与最低点的坐标分别为M( ,求此函数的解析式及单调递增区间。
,求此函数的解析式及单调递增区间。
设 是三角形的内角,且
是三角形的内角,且 和
和 是关于
是关于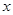 方程
方程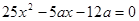 的两个根。
的两个根。
(1)求 的值;
的值;
(2)求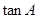 的值.
的值.
设函数f(x)=sin(2x+φ),(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
(Ⅰ)求φ;
(Ⅱ)求函数y=f(x)的单增区间;
(Ⅲ)证明直线5x-2y+c=0与函数y=f(x)的图像不相切.
若向量 ,
, 其中
其中 ,记函数
,记函数 ,若函数
,若函数 的图像与直线
的图像与直线 (
( 为常数)相切,并且切点的横坐标依次成公差为
为常数)相切,并且切点的横坐标依次成公差为 的等差数列。
的等差数列。
(1)求 的表达式及
的表达式及 的值;
的值;
(2)将函数 的图像向左平移
的图像向左平移 ,得到
,得到 的图像,当
的图像,当 时,
时, 的交点横坐标成等比数列,求钝角
的交点横坐标成等比数列,求钝角 的值。
的值。
已知:函数 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求 函 数 的 解 析 式;
的 解 析 式;
(Ⅱ)在△ 中,角
中,角 的 对 边 分 别是
的 对 边 分 别是 ,若
,若 的 取 值 范 围.
的 取 值 范 围.