高中数学几何不等式试题

已知|a|＜1,|b|＜1,|c|＜1,求证: abc+2＞a+b+c.

设a，b∈R，定义运算“∧”和“∨”如下：
a∧b＝a∨b＝
若正数a，b，c，d满足ab≥4，c＋d≤4，则(  )

A．a∧b≥2，c∧d≤2	B．a∧b≥2，c∨d≥2
C．a∨b≥2，c∧d≤2	D．a∨b≥2，c∨d≥2

下列四个命题中:①a+b≥2 ②sin²x+≥4 ③设x，y都是正数，若=1，则x+y的最小值是12 ④若|x－2|＜ε，|y－2|＜ε，则|x－y|＜2ε，其中所有真命题的序号是__________.

若a,b,c＞0且a(a+b+c)+bc=4-2,则2a+b+c的最小值为

A．-1

B．+1

C．2+2

D．2-2

实数a_i（i=1,2,3,4,5,6）满足（a₂－a₁）²+（a₃－a₂）²+（a₄－a₃）²+（a₅－a₄）²+（a₆－a₅）²=1则（a₅+a₆）－（a₁+a₄）的最大值为（　　　）

A．3

B．2

C．

D．1

若，且，则下列不等式中能恒成立的是　　　　　(    )

A．．

B．．

C．．

D．．

若不等式(mx－1)［3m ²－( x + 1)m－1］≥0对任意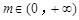恒成立，则实数x的值为    ．

下列说法：
①命题“”的否定是“”；
②关于的不等式恒成立，则的取值范围是；
③对于函数，则有当时，，使得函数在上有一个零点；
④已知，且是常数，又的最小值是，则.
其中错误的是            ．（填写所有符合题意的序号）

已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.

已知a ,b ,m∈R ，则下面推理中正确的是（ ）                      

A．a>b	B．
C．	D．

设，则的最小值是          

证明：

（1）解关于不等式．
（2）证明：（其中）．

已知不等式的解集为，点在直线上，其中，则的最小值为（  ）

A．

B．8

C．9

D．12

关于x的不等式x²－ax＋2a＜0的解集为A，若集合A中恰有两个整数，则实数a的取值范围是________．