高中数学几何不等式试题

已知f(x)=则不等式x+x·f(x)≤2的解集是　　　　.

已知函数f(x)＝|ln x|，若 >a>b>1，则f(a)，f(b)，f(c)比较大小关系正确的是(  )．

A．f(c)>f(b)>f(a)	B．f(b)>f(c)>f(a)
C．f(c)>f(a)>f(b)	D．f(b)>f(a)>f(c)

若不等式a·4^x-2^x+1>0对一切x∈R恒成立,则实数a的取值范围是　　　　.

下列不等式中，与不等式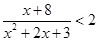解集相同的是（    ）

A．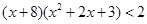

B．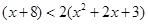

C．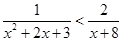

D．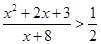

对于实数x,当n≤x<n+1(n∈Z)时,规定[x]=n,则不等式4[x]²-36[x]+45<0的解集为(　　)

A．{x|2≤x<8}	B．{x|2<x≤8}
C．{x|2≤x≤8}	D．{x|2<x<8}

设a,b为正实数.现有下列命题:
①若a²-b²=1,则a-b<1;
②若-=1,则a-b<1;
③若|-|=1,则|a-b|<1;
④若|a³-b³|=1,则|a-b|<1.
其中的真命题有　　　　.(写出所有真命题的编号)

已知x,y为正实数,满足1≤lg(xy)≤2,3≤lg≤4,求lg(x⁴y²)的取值范围.

己知，若恒成立，利用柯西不等式可求得实数的取值范围是         .

若<<0,则下列不等式:①<;②|a|+b>0;③a->b-;④lna²>lnb²中,正确的是(　　)

A．①④

B．②③

C．①③

D．②④

设0≤α≤π,不等式8x²-(8sinα)x+cos2α≥0对x∈R恒成立,则α的取值范围为　　　　.

函数（-2<<2）的最小值为              ．

关于x的不等式ax+b>0的解集不可能是（ ）

A．R

B．

C．

D．

已知，若存在，使得任意恒成立，且两边等号能取到，则的最小值为          .

设P=,Q=-,R=-,则P,Q,R的大小顺序是　　　　　.

若函数的定义域为，则实数的取值范围是（   ）

A．	B．
C．	D．