如果定义在R上的函数 对任意两个不等的实数
对任意两个不等的实数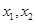 都有
都有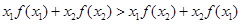 ,则称函数
,则称函数 为“
为“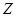 函数”给出函数:
函数”给出函数: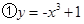 ,
,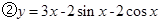
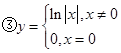
 。
。
以上函数为“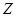 函数”的序号为
函数”的序号为
(本小题满分14分)
若函数 对任意的实数
对任意的实数 ,
, ,均有
,均有 ,则称函数
,则称函数 是区间
是区间 上的“平缓函数”.
上的“平缓函数”.
(1) 判断 和
和 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;
(2) 若数列 对所有的正整数
对所有的正整数 都有
都有  ,设
,设 ,
,
求证:  .
.
(本小题满分14分)对定义域分别是 、
、 的函数
的函数 、
、 ,
,
规定:函数
已知函数 ,
,
 .
.
(1)求函数 的解析式;
的解析式;
⑵对于实数 ,函数
,函数 是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.
是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.
(本题满分14分) 已知 是方程
是方程 的两个不等实根,函数
的两个不等实根,函数 的定义域为
的定义域为 .
.
⑴当 时,求函数
时,求函数 的值域;
的值域;
⑵证明:函数 在其定义域
在其定义域 上是增函数;
上是增函数;
⑶在(1)的条件下,设函数 ,
,
若对任意的 ,总存在
,总存在 ,使得
,使得 成立,
成立,
求实数 的取值范围.
的取值范围.
已知定义域为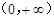 的函数
的函数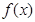 满足:①对任意
满足:①对任意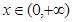 ,恒有
,恒有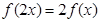 成立;当
成立;当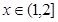 时,
时,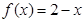 。给出如下结论:
。给出如下结论:
①对任意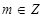 ,有
,有 ;②函数
;②函数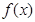 的值域为
的值域为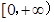 ;③存在
;③存在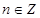 ,使得
,使得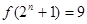 ;④“函数
;④“函数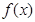 在区间
在区间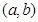 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在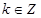 ,使得
,使得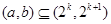 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。
(本小题满分12分)
已知函数
(1)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(2)当 时,求
时,求 在
在 上的最大值和最小值;
上的最大值和最小值;
(3) 当 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数 ,都有
,都有 。
。