2013年高考数学预测题 第三期(2013年4月上)
设命题甲为: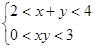 ,设命题乙为:
,设命题乙为: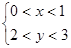 ,那么甲是乙的( )
,那么甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在如下图所示的坐标平面的可行域内(阴影部分且包括边界),目标函数:z=x+ay取得最小值的最优解有无数个,则 的最大值是 ( )
的最大值是 ( )
| A.2 | B.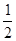 |
C.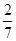 |
D.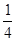 |
从10名大学生村官中选3个人担任乡长助理,则甲、丙至少有1人人选,而乙没有人选的不同选法的种数位为
| A. 85 | B. 56 | C. 49 | D. 28 |
已知函数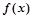 定义在R上的奇函数,当
定义在R上的奇函数,当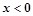 时,
时,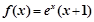 ,给出下列命题:
,给出下列命题:
①当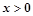 时,
时,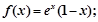 ②函数
②函数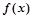 有2个零点
有2个零点
③ 的解集为
的解集为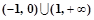 ④
④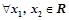 ,都有
,都有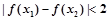
其中正确命题个数是:
| A.1 | B.2 | C.3 | D.4 |
已知P为椭圆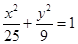 上一点,F1,F2是椭圆的焦点,∠F1PF2=900,则△F1PF2的面积为___________。
上一点,F1,F2是椭圆的焦点,∠F1PF2=900,则△F1PF2的面积为___________。
已知定义域为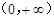 的函数
的函数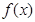 满足:①对任意
满足:①对任意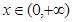 ,恒有
,恒有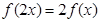 成立;当
成立;当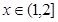 时,
时,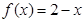 。给出如下结论:
。给出如下结论:
①对任意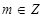 ,有
,有 ;②函数
;②函数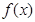 的值域为
的值域为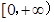 ;③存在
;③存在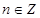 ,使得
,使得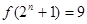 ;④“函数
;④“函数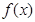 在区间
在区间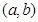 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在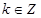 ,使得
,使得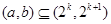 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。
(本小题满分12分)
已知向量 ,设函数
,设函数 +1
+1
(1)若 ,
,  ,求
,求 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
在一次人才招聘会上,有 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
(1)求该技术人员被录用的概率;
(2)设 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求 的分布列和数学期望.
的分布列和数学期望.
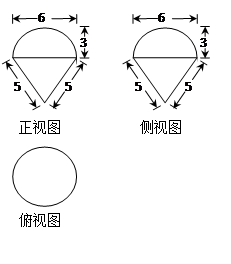
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
(1)当AA1=3,AB=2,AD=2,求AC1的长;
(2)当底面ABCD是菱形时,求证:
(本小题满分12分)某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
, 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
(本题12分)已知函数, 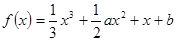
(Ⅰ)设函数f(x)的图象与x轴交点为A, 曲线y=f(x)在A点处的切线方程是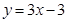 , 求
, 求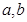 的值;
的值;
(Ⅱ)若函数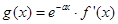 , 求函数
, 求函数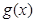 的单调区间.
的单调区间.
 ,
,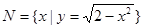 ,则
,则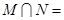 ( )
( )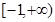
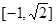
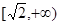
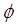
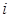 是虚数单位,则
是虚数单位,则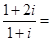 ( )
( )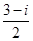
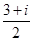
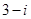
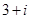
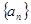 为等差数列,公差
为等差数列,公差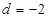 ,
,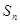 为其前
为其前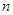 项和,若
项和,若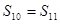 ,则
,则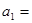 ( )
( )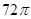
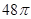
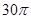
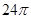
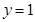 与曲线
与曲线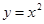 所围成的封闭图形的面积是
所围成的封闭图形的面积是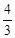
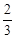
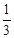

 与直线
与直线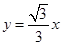 的位置关系是( )
的位置关系是( )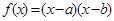 (其中
(其中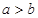 )的图象如下图所示,则函数
)的图象如下图所示,则函数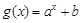 的图象是
的图象是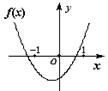
 定义域为R,则
定义域为R,则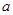 的取值范围是________.
的取值范围是________.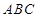 中,设三个内角
中,设三个内角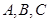 对应的边长分别为
对应的边长分别为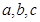 ,且
,且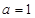 ,
,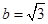 ,
,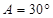 ,则
,则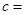 .
.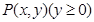 为平面直角坐标系
为平面直角坐标系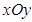 中的一个动点(其中O为坐标原点),点P到定点
中的一个动点(其中O为坐标原点),点P到定点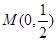 的距离比点P到
的距离比点P到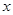 轴的距离大
轴的距离大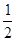 .
. 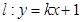 与点P的轨迹相交于A、B两点,且
与点P的轨迹相交于A、B两点,且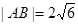 ,求
,求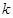 的值.
的值.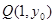 是曲线C上的一点,求以Q为切点的曲线C 的切线方程.
是曲线C上的一点,求以Q为切点的曲线C 的切线方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号