高中数学函数迭代试题

关于的函数，有下列结论：
①、该函数的定义域是；            ②、该函数是奇函数；
③、该函数的最小值为；
④、当 时为增函数，当时为减函数；
其中，所有正确结论的序号是            。

已知函数是R上的可导函数，当时，有,则函数的零点个数是(     )

A．0

B．1

C．2

D．3

设，.
（1）若恒成立，求实数的取值范围；
（2）若时，恒成立，求实数的取值范围；
（3）当时，解不等式.

把函数的图像向左平移个单位，所得图像的解析式是（     ）

A．	B．
C．	D．

已知函数是偶函数，在内单调递减，则实数            。

已知   
（1）画出的草图；
（2）由图象指出的单调区间；
（3）设 证明：

对函数 ，若存在 且 ，使得 （其中 A， B为常数），则称 为"可分解函数"。
（1）试判断 是否为"可分解函数"，若是，求出 A， B的值；若不是，说明理由；
（2）用反证法证明： 不是"可分解函数"；
（3）若 是"可分解函数"，则求 a的取值范围，并写出 A， B关于 a的相应的表达式。

下列函数是奇函数的是 (　 　)

A．

B．

C．

D．

（本题14分）
已知是一个奇函数.
（1）求的值和的值域；
（2）设>,若在区间是增函数，求的取值范围
（3） 设，若对取一切实数，不等式都成立，求的取值范围．

已知函数，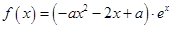
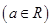
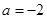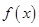(1)当时，求函数的极值；
(2) 若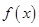在[-1，1]上单调递减，求实数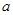的取值范围.

已知函数
（1）当时，求函数极小值；
（2）试讨论曲线与轴公共点的个数。

已知函数 f（x）的定义域为，其导函数f＇（x）的图象如图所示，则对于任意，下列结论正确的是(     )

①恒成立；
②；
③；
④ > ；
⑤ < ．

A．①③

B．①③④

C．②④

D．②⑤

已知函数在处取得极小值2．
（1）求函数的解析式；
（2）求函数的极值；
（3）设函数，若对于任意，总存在，使得，求实数的取值范围．

设函数
（1）设，，证明：在区间内存在唯一的零点；
（2）设为偶数，，，求的最小值和最大值；
（3）设，若对任意，有，求的取值范围；

已知函数f（x）=1n（2ax+1）+－x²－2ax（a∈R）．
（1）若y=f（x）在[4，+∞）上为增函数，求实数a的取值范围；
（2）当a=时，方程f（1－x）=有实根，求实数b的最大值．