对函数  ,若存在
,若存在 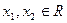 且
且 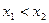 ,使得
,使得  (其中 A, B为常数),则称
(其中 A, B为常数),则称  为"可分解函数"。
为"可分解函数"。
(1)试判断 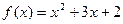 是否为"可分解函数",若是,求出 A, B的值;若不是,说明理由;
是否为"可分解函数",若是,求出 A, B的值;若不是,说明理由;
(2)用反证法证明:  不是"可分解函数";
不是"可分解函数";
(3)若  是"可分解函数",则求 a的取值范围,并写出 A, B关于 a的相应的表达式。
是"可分解函数",则求 a的取值范围,并写出 A, B关于 a的相应的表达式。
相关知识点
推荐套卷
对函数  ,若存在
,若存在 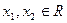 且
且 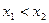 ,使得
,使得  (其中 A, B为常数),则称
(其中 A, B为常数),则称  为"可分解函数"。
为"可分解函数"。
(1)试判断 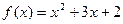 是否为"可分解函数",若是,求出 A, B的值;若不是,说明理由;
是否为"可分解函数",若是,求出 A, B的值;若不是,说明理由;
(2)用反证法证明:  不是"可分解函数";
不是"可分解函数";
(3)若  是"可分解函数",则求 a的取值范围,并写出 A, B关于 a的相应的表达式。
是"可分解函数",则求 a的取值范围,并写出 A, B关于 a的相应的表达式。