高中数学函数迭代试题

(12分) 已知函数。
（1）求函数y=的零点；
（2） 若y=的定义域为[3，9]， 求的最大值与最小值。

函数在[0，3]上的最大值、最小值分别是（ ）

A．-4，-15

B．5，-4

C．5，-15

D．5，-16

将函数的图像向左平移2个单位得到函数的图像，则函数的解析表达式为                .

已知,用符号表示不超过的最大整数。函数有且仅有3个零点，则的取值范围是__________.

（本小题满分12分）
设函数f (x)＝，其中a∈R．
（1）若a＝1，f (x)的定义域为［0，3］，求f (x)的最大值和最小值．
（2）若函数f (x)的定义域为区间（0，＋∞），求a的取值范围使f (x)在定义域内是单调减函数．

（本小题满分14分）
设函数
（I）求函数在区间[0，1]上的最小值；
（II）当时，记曲线在点处的切线为与x轴交于点，求证：

已知函数满足，且时，，则与的图象的交点个数为（  ）

A．3

B．4

C．5

D．6

设（其中，，为常数），若。则等于（   ）

A．31

B．17

C．－31

D．24

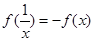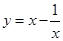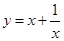具有性质：的函数，我们称为满足“倒负”变换的函数，下列函数：①；②；③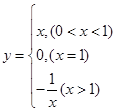中满足“倒负”变换的函数是（  ）

A．①②

B．①③

C．②③

D．只有①

若函数是定义在上的偶函数，在上是减函数，且，则使得的的取值范围是（    ）

A．	B．
C．	D．

对于函数f (x)和g(x)，其定义域为[a, b]，若对任意的x∈[a, b]总有|1－|≤，则称f (x)可被g(x)置换，那么下列给出的函数中能置换f (x)= x∈[4，16]的是 (    )

A．g(x)=2x+6 x∈[4，16]	B．g(x)=x^2+9 x∈[4，16]
C．g(x)= (x+8) x∈[4，16]	D．g(x)=(x+6) x∈[4，16]

已知函数，且在处取得极值.
（1）求的值；
（2）若当时，恒成立，求的取值范围；
（3）对任意的是否恒成立？如果成立，给出证明，如果不成立，请说明理由.

已知函数
（1）当时，求函数极小值；
（2）试讨论曲线与轴公共点的个数。

(本小题满分12分)
已知函数是定义域为的奇函数，（1）求实数的值；（2）证明是上的单调函数；（3）若对于任意的，不等式恒成立，求的取值范围．

已知函数，，且，当时，是增函数，设，，，则、 、的大小顺序是（   ）。

A．

B．

C．

D．