【原创】如果对定义在 上的函数
上的函数 ,对任意
,对任意 ,都有
,都有 ,
,
则称函数 为“
为“ 函数”.给出下列四个函数:
函数”.给出下列四个函数:
① ;②
;② ;③
;③ ;④
;④ .
.
则其中“ 函数”共有( )
函数”共有( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
(本小题满分12分)
若函数 满足下列两个性质:
满足下列两个性质:
① 在其定义域上是单调增函数或单调减函数;
在其定义域上是单调增函数或单调减函数;
②在 的定义域内存在某个区间使得
的定义域内存在某个区间使得 在
在 上的值域是
上的值域是 .则我们称
.则我们称 为“内含函数”.
为“内含函数”.
(1)判断函数 是否为“内含函数”?若是,求出a、b,若不是,说明理由;
是否为“内含函数”?若是,求出a、b,若不是,说明理由;
(2)若函数 是“内含函数”,求实数t的取值范围.
是“内含函数”,求实数t的取值范围.
设 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若函数
上的两个函数,若函数 上有两个不同的零点,则称
上有两个不同的零点,则称 和
和 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”。若
称为“关联区间”。若 上是“关联函数”,则m的取值范围为( )
上是“关联函数”,则m的取值范围为( )
A. |
B. |
C. |
D. |
函数 的定义域为A,若
的定义域为A,若 且
且
 时总有
时总有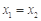 ,则称
,则称 为单函数.例如,函数
为单函数.例如,函数 =2x+1(
=2x+1( )是单函数.下列命题:
)是单函数.下列命题:
①函数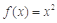 (x
(x R)是单函数;
R)是单函数;
②指数函数 (x
(x R)是单函数;
R)是单函数;
③若 为单函数,
为单函数, 且
且 ,则
,则 ;
;
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
若函数 y =f(x)在定义域内给定区间[a,b]上存在xo(a<xo<b),满足f(xo)= ,则称函数y=f(x)是[a,b]上的“平均值函数”,xo是它的一个均值点.例如y=|x|是[-2,2]上的“平均值函数”,O就是它的均值点.
,则称函数y=f(x)是[a,b]上的“平均值函数”,xo是它的一个均值点.例如y=|x|是[-2,2]上的“平均值函数”,O就是它的均值点.
(1)若函数,f(x)= x2-mx-1是[-1,1]上的“平均值函数”,则实数m的取值范围是 .
(2)若f(x)=㏑x是区间[a,b](b>a≥1)上的“平均值函数”,xo是它的一个均值点,则㏑xo与 的大小关系是 .
的大小关系是 .
已知函数 ,
, .定义:
.定义: ,
, ,……,
,……,
 ,
, …满足
…满足 的点
的点 称为
称为 的
的 阶不动点.则
阶不动点.则 的n
的n
阶不动点的个数是( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
已知 ,
, 是定义在集合
是定义在集合 上的两个函数.对任意的
上的两个函数.对任意的 ,存在常数
,存在常数 ,使得
,使得 ,
, ,且
,且 .则函数
.则函数
在集合 上的最大值为( )
上的最大值为( )
A. |
B. |
C. |
D. |
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间 为函数
为函数 的一个“可等域区间”.给出下列 4个函数:
的一个“可等域区间”.给出下列 4个函数:
① ,②
,② ,③
,③ ,④
,④ .
.
其中存在唯一“可等域区间”的“可等域函数”为
| A.①②③ | B.②③ | C.①③ | D.②③④ |
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则关于函数
为有理数集,则关于函数 有如下四个结论:
有如下四个结论:
① ;
;
②函数 是偶函数;
是偶函数;
③任取一个不为零的有理数 ,
, 对任意的
对任意的 恒成立;
恒成立;
④存在三个点 ,
, ,
, ,使得
,使得 为等边三角形.
为等边三角形.
其中正确结论的个数是( )
A. |
B. |
C. |
D. |
对于定义域和值域均为[0,1]的函数f(x),定义 ,
, ,…,
,…, ,n=1,2,3,….满足
,n=1,2,3,….满足 的点x∈[0,1]称为f的
的点x∈[0,1]称为f的 阶周期点.设
阶周期点.设 则f的
则f的 阶周期点的个数是
阶周期点的个数是
| A.2n | B.2(2n-1) | C.2n | D.2n2 |
若函数 满足:在定义域D内存在实数
满足:在定义域D内存在实数 ,使得
,使得 成立,则称函数
成立,则称函数 为“1的饱和函数”.给出下列四个函数:①
为“1的饱和函数”.给出下列四个函数:① ;②
;② ;③
;③ ;④
;④ .其中是“1的饱和函数”的所有函数的序号为( ).
.其中是“1的饱和函数”的所有函数的序号为( ).
| A.①③ | B.②④ | C.①② | D.③④ |
(本小题满分16分)对于函数 ,如果存在实数
,如果存在实数 使得
使得 ,那么称
,那么称 为
为 的生成函数.
的生成函数.
(1)下面给出两组函数, 是否分别为
是否分别为 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: ;
;
第二组: ;
;
(2)设 ,生成函数
,生成函数 .若不等式
.若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
对于三次函数 ,给出定义:设
,给出定义:设 是函数y=f(x)的导数,
是函数y=f(x)的导数, 是
是 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.
为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.
设函数 ,则
,则 =( )
=( )
| A.2014 | B.2013 | C. |
D.1007 |