【改编题】已知[x]表示不超过实数x的最大整数(x∈R),如:[﹣1.3]=﹣2,[0.8]=0,[3.4]=3.定义{x}=x﹣[x],求{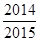 }+{
}+{ }+{
}+{ }+…+{
}+…+{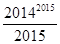 }=
}=
我们称满足下面条件的函数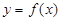 为“
为“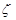 函数”:存在一条与函数
函数”:存在一条与函数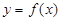 的图象有两个不同交点(设为
的图象有两个不同交点(设为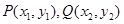 )的直线,
)的直线,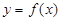 在
在 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数:
①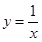 ②
②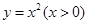 ③
③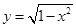 ④
④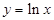 ,
,
其中为“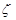 函数”的是(将所有你认为正确的序号填在横线上)
函数”的是(将所有你认为正确的序号填在横线上)
我们称满足下面条件的函数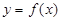 为“
为“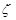 函数”:存在一条与函数
函数”:存在一条与函数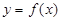 的图象有两个不同交点(设为
的图象有两个不同交点(设为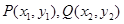 )的直线,
)的直线,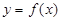 在
在 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数:
①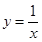 ②
②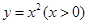 ③
③ ④
④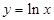 ,
,
其中为“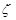 函数”的是(将所有你认为正确的序号填在横线上)
函数”的是(将所有你认为正确的序号填在横线上)
定义:如果函数 在定义域内给定区间
在定义域内给定区间 上存在
上存在
 ,满足
,满足 ,则称函数
,则称函数 是
是 上的“平均值函数”,
上的“平均值函数”, 是它的一个均值点,例如
是它的一个均值点,例如 是
是 上的平均值函数,
上的平均值函数, 就是它的均值点.现有函数
就是它的均值点.现有函数 是
是 上的平均值函数,则实数
上的平均值函数,则实数 的取值范围是.
的取值范围是.
【原创】如果对定义在R上的函数 ,对任意两个不相等的实数
,对任意两个不相等的实数 都有
都有 ,则称函数
,则称函数 为“M函数”.
为“M函数”.
给出下列函数:
① ;②
;② ;③
;③ ;④
;④ .
.
以上函数是“M函数”的所有序号为__________(把所有正确命题的序号都填上).
对定义在区间D上的函数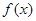 和
和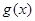 ,如果对任意
,如果对任意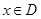 ,都有
,都有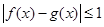 成立,那么称函数
成立,那么称函数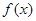 在区间D上可被
在区间D上可被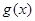 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①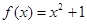 在区间
在区间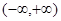 上可被
上可被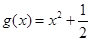 替代;
替代;
②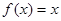 可被
可被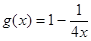 替代的一个“替代区间”为
替代的一个“替代区间”为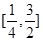 ;
;
③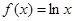 在区间
在区间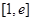 可被
可被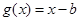 替代,则
替代,则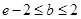 ;
;
④ ,则存在实数
,则存在实数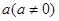 ,使得
,使得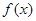 在区间
在区间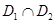 上被
上被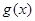 替代;
替代;
其中真命题的有
对于三次函数 ,定义
,定义 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数都关于点 对称:
对称:
②存在三次函数 有实数解
有实数解 ,点
,点 为函数
为函数 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则
,则
其中正确命题的序号为____________________(把所有正确命题的序号都填上).
函数 的定义域为A,若
的定义域为A,若 且
且
 时总有
时总有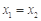 ,则称
,则称 为单函数.例如,函数
为单函数.例如,函数 =2x+1(
=2x+1( )是单函数.下列命题:
)是单函数.下列命题:
①函数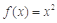 (x
(x R)是单函数;
R)是单函数;
②指数函数 (x
(x R)是单函数;
R)是单函数;
③若 为单函数,
为单函数, 且
且 ,则
,则 ;
;
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
【原创】对定义在区间D上的函数 和
和 ,如果对任意
,如果对任意 ,都有
,都有 成立,那么称函数
成立,那么称函数 在区间D上可被
在区间D上可被 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
① 在区间
在区间 上可被
上可被 替代;
替代;
② 可被
可被 替代的一个“替代区间”为
替代的一个“替代区间”为 ;
;
③ 在区间
在区间 可被
可被 替代,则
替代,则 ;
;
④ ,则存在实数
,则存在实数 ,使得
,使得 在区间
在区间 上被
上被 替代;
替代;
其中真命题的有
对于定义在 上的函数
上的函数 ,若存在距离为
,若存在距离为 的两条直线
的两条直线 和
和 ,使得对任意
,使得对任意 都有
都有 恒成立,则称函数
恒成立,则称函数 有一个宽度为
有一个宽度为 的通道.给出下列函数:
的通道.给出下列函数:
① ;②
;② ;③
;③ ;④
;④
其中在区间 上通道宽度可以为
上通道宽度可以为 的函数有 (写出所有正确的序号).
的函数有 (写出所有正确的序号).
【原创】已知函数f(x)定义域为D,若∀a,b,c∈D,f(a),f(b),f(c)都是某一三角形的三边,则称f(x)为定义在D上的“保三角形函数”,以下说法正确的是 .
①f(x)=2(x∈R)不是R上的“保三角形函数”
②若定义在R上的函数f(x)的值域为[ ,2],则f(x)一定是R上的“保三角形函数”
,2],则f(x)一定是R上的“保三角形函数”
③f(x)= 是其定义域上的“保三角形函数”
是其定义域上的“保三角形函数”
④当t>1时,函数f(x)=ex+t一定是[0,1]上的“保三角形函数”