对于函数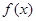
，若存在区间
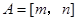，使得
，则称函数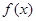为“可等域函数”，区间
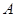为函数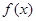的一个“可等域区间”．给出下列 4个函数：
①
，②
，③
，④
．
其中存在唯一“可等域区间”的“可等域函数”为
| A．①②③ | B．②③ | C．①③ | D．②③④ |
项的和
等于
( )
均为锐角，且
则△ABC的形状是（）
，
，则
（）
得（）
是
上的偶函数，则
的值是（）
相关知识点
推荐套卷
对于函数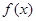，若存在区间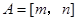，使得，则称函数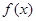为“可等域函数”，区间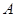为函数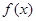的一个“可等域区间”．给出下列 4个函数：
①，②，③，④．
其中存在唯一“可等域区间”的“可等域函数”为
| A．①②③ | B．②③ | C．①③ | D．②③④ |
粤公网安备 44130202000953号