高中数学函数迭代填空题

分解因式=                           ．

已知函数在R是奇函数，且当时，，则时，的解析式为____   ___________

已知函数在R上为增函数，且满足，则的取值范围是___________．

当时，不等式恒成立，则的取值范围是          .

若满足对于时有恒成立，则称函数在上是“被k限制”，若函数在区间上是“被2限制”的，则的取值范围为            .

小于100的自然数中被7除余3的所有数的和是       .

定义在上的函数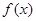同时满足性质：①对任何，均有成立；②对任何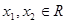，当且仅当时，有.则的值为                .

已知函数满足：，，则=_____________.

设函数的定义域为，若存在非零实数使得对于任意，有，且，则称为上的高调函数.如果定义域是的函数为上的高调函数，那么实数的取值范围是　  .     

设定义在上的函数，若函数与的定义域与值域都相同，则实数的取值范围为         ．

设f(x)＝，若f(f(1))＝1，则a＝________.

设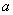是实数．若函数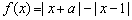是定义在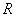上的奇函数，但不是偶函数，则函数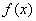的递增区间为__________;

在弹性限度内，拉伸弹簧所用的力与弹簧伸长的长度成正比．如果的力能使弹簧伸长，则把弹簧从平衡位置拉长（在弹性限度内）时所做的功为     （单位：焦耳）.

已知函数的定义域为，部分对应值如下表，的导函数的图象如图所示. 下列关于的命题：

①函数的极大值点为，；②函数在上是减函数；③如果当时，的最大值是2，那么的最大值为4；
④当时，函数有个零点；⑤函数的零点个数可能为0、1、2、3、4个．其中正确命题的序号是                           ．

已知函数是上的偶函数，若对于，都有，且当时， ，的值为             ．