已知函数 ,给出下列四个说法:
,给出下列四个说法:
①若 ,则
,则 ,②点
,②点 是
是 的一个对称中心,
的一个对称中心,
③ 在区间
在区间 上是增函数,④
上是增函数,④ 的图象关于直线
的图象关于直线 对称.
对称.
其中正确说法的序号是 .(只填写序号)
已知函数 ,(
,( ,
, .若
.若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,并在
对称,并在 处取得最小值,则正实数
处取得最小值,则正实数 的值构成的集合是 .
的值构成的集合是 .
若函数f(x)在定义域D内某区间I上是增函数,且 在I上是减函数,则称y=f(x)在I 上是“弱增函数”.已知函数h(x)=x2-(b-1)x+b在(0,1]上是“弱增函数”,则实数b的值为 .
在I上是减函数,则称y=f(x)在I 上是“弱增函数”.已知函数h(x)=x2-(b-1)x+b在(0,1]上是“弱增函数”,则实数b的值为 .
对于函数 ,若存在区间
,若存在区间 =[
=[ ](
]( ),使得
),使得 ,则称区间
,则称区间 为函数
为函数 的一个“稳定区间”.给出下列四个函数:
的一个“稳定区间”.给出下列四个函数:
① ②
② ③
③ ④
④
其中存在“稳定区间”的函数有_____________(填正确序号).
设函数 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为
为 上的
上的 高调函数,如果定义域为
高调函数,如果定义域为 的函数
的函数 是奇函数,当
是奇函数,当 时,
时, =
= ,且
,且 为
为 上的
上的 高调函数,那么实数
高调函数,那么实数 的取值范围是
的取值范围是
对于定义域为 的函数
的函数 ,若存在区间
,若存在区间 ,使得
,使得 则称区间M为函数
则称区间M为函数 的“等值区间”.给出下列三个函数:
的“等值区间”.给出下列三个函数:
① ; ②
; ② ; ③
; ③
则存在“等值区间”的函数的个数是___________.
已知函数 及其导数
及其导数 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是
是 的一个“巧值点”,下列函数中,有“巧值点”的是 (填上正确的序号)
的一个“巧值点”,下列函数中,有“巧值点”的是 (填上正确的序号)
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)
已知 ,且方程
,且方程 无实数根,下列命题:
无实数根,下列命题:
①方程 也一定没有实数根;
也一定没有实数根;
②若 ,则不等式
,则不等式 对一切实数
对一切实数 都成立;
都成立;
③若 ,则必存在实数
,则必存在实数 ,使
,使
④若 ,则不等式
,则不等式 对一切实数
对一切实数 都成立.
都成立.
其中正确命题的序号是 .
定义域为 的函数
的函数 的图像的两个端点为
的图像的两个端点为 ,
, 是
是 图像上任意一点,其中
图像上任意一点,其中 ,向量
,向量 ,若不等式
,若不等式 恒成立,则称函数
恒成立,则称函数 在
在 上“
上“ 阶线性近似”,若函数
阶线性近似”,若函数 在
在 上“
上“ 阶线性近似”,则实数
阶线性近似”,则实数 的取值范围是
的取值范围是
已知定义域为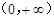 的函数
的函数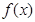 满足:①对任意
满足:①对任意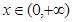 ,恒有
,恒有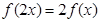 成立;当
成立;当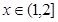 时,
时,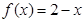 。给出如下结论:
。给出如下结论:
①对任意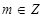 ,有
,有 ;②函数
;②函数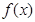 的值域为
的值域为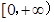 ;③存在
;③存在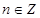 ,使得
,使得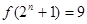 ;④“函数
;④“函数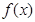 在区间
在区间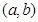 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在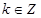 ,使得
,使得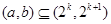 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。