湖北省咸宁市高三三校联考理科数学试卷
已知函数 向左平移
向左平移 个单位后,得到函数
个单位后,得到函数 ,下列关于
,下列关于 的说法正确的是( )
的说法正确的是( )
A.图象关于点 中心对称 中心对称 |
B.图象关于 轴对称 轴对称 |
C.在区间 单调递增 单调递增 |
D.在 单调递减 单调递减 |
下列说法中,正确的是( )
A.命题“若 ,则 ,则 ”的逆命题是真命题 ”的逆命题是真命题 |
B.命题“存在 ”的否定是:“任意 ”的否定是:“任意 ” ” |
C.命题“ 或 或 ”为真命题,则命题“ ”为真命题,则命题“ ”和命题“ ”和命题“ ”均为真命题 ”均为真命题 |
D.已知 则“ 则“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点 为中心﹐其中
为中心﹐其中 ,分别为原点
,分别为原点 到两个顶点的向量﹒若将原点
到两个顶点的向量﹒若将原点 到正六角星12个顶点的向量﹐都写成为
到正六角星12个顶点的向量﹐都写成为 的形式﹐则
的形式﹐则 的最大值为( ).
的最大值为( ).
| A.2 | B.3 | C.4 | D.5 |
对于函数 和
和 ,设
,设 ,
, ,若存在
,若存在 、
、 ,使得
,使得 ,则称
,则称 互为“零点关联函数”.若函数
互为“零点关联函数”.若函数 与
与 互为“零点关联函数”,则实数
互为“零点关联函数”,则实数 的取值范围为( ).
的取值范围为( ).
A. |
B. |
C. |
D. |
如图,互不相同的点 和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=
和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn= ,若
,若 =1,
=1, =2,则
=2,则 =
= 
定义域为 的函数
的函数 的图像的两个端点为
的图像的两个端点为 ,
, 是
是 图像上任意一点,其中
图像上任意一点,其中 ,向量
,向量 ,若不等式
,若不等式 恒成立,则称函数
恒成立,则称函数 在
在 上“
上“ 阶线性近似”,若函数
阶线性近似”,若函数 在
在 上“
上“ 阶线性近似”,则实数
阶线性近似”,则实数 的取值范围是
的取值范围是
已知函数 及其导数
及其导数 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是
是 的一个“巧值点”,下列函数中,有“巧值点”的是 (填上正确的序号)
的一个“巧值点”,下列函数中,有“巧值点”的是 (填上正确的序号)
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)
(本小题满分11分)已知函数
(1)求函数 的最小值;
的最小值;
(2)已知 ,命题
,命题 关于
关于 的不等式
的不等式 对任意
对任意 恒成立;命题
恒成立;命题 函数
函数 是增函数,若“
是增函数,若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知向量 函数
函数
(1)求函数 的最小正周期
的最小正周期 ;
;
(2)已知 分别为
分别为 内角
内角 的对边,其中
的对边,其中 为锐角,
为锐角, ,且
,且 ,求
,求 的面积
的面积
(本小题满分12分)已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,且满足
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,且满足 ,记
,记
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 .求不超过
.求不超过 的最大整数.
的最大整数.
(本小题满分14分)某商场预计2015年从1月起前 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量 (单位:件)
(单位:件)
(1)写出第 个月的需求量
个月的需求量 的表达式;
的表达式;
(2)若第 个月的销售量
个月的销售量 (单位:件),每件利润
(单位:件),每件利润 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: )
)
 ,
, ,则
,则 等于( )
等于( )



 满足
满足 ,则
,则 ( )
( )



 ,若
,若 与
与 共线,则
共线,则 的值为( )
的值为( )



 对任意的
对任意的 ,满足
,满足 ,且
,且 ,那么
,那么 等于( )
等于( ) ,则
,则 的值为 ( )
的值为 ( )



 ,则下列函数的图象错误的是( ).
,则下列函数的图象错误的是( ).
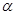 为第二象限角,
为第二象限角,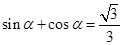 ,则
,则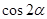 =___________;
=___________; 为
为 的重心,若
的重心,若 则
则

 时,求
时,求 的最值;
的最值; ,求
,求 的值
的值 .
. 在
在 处有极值,求函数
处有极值,求函数 ,使得关于
,使得关于 的不等式
的不等式 在
在 上恒成立?若存在,求出
上恒成立?若存在,求出 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号