（本小题满分14分）某商场预计2015年从1月起前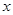
个月顾客对某种商品的需求总量
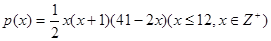（单位：件）
（1）写出第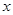个月的需求量
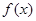的表达式；
（2）若第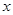个月的销售量
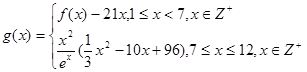（单位:件），每件利润
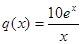（单位：元），求该商场销售该商品，预计第几个月的月利润达到最大值？月利润的最大值是多少？（参考数据：
）
相关试题
的值；
，求
的值.
是首项为
，公比
的等比数列.设
，
，数列
满足
；
成等差数列；
项和
；
对一切正整数
的取值范围.
在点
处的切线方程；
的极值；
恒成立，求实数
的取值范围.
，函数
.
的值；
的单调区间.
的前
项和为
，公差
，
，且
成等比数列.
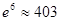的前推荐套卷
（本小题满分14分）某商场预计2015年从1月起前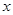个月顾客对某种商品的需求总量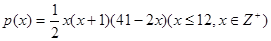（单位：件）
（1）写出第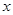个月的需求量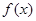的表达式；
（2）若第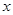个月的销售量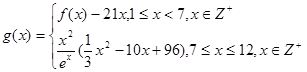（单位:件），每件利润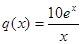（单位：元），求该商场销售该商品，预计第几个月的月利润达到最大值？月利润的最大值是多少？（参考数据：）
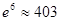粤公网安备 44130202000953号