已知点 是函数
是函数 的图象上任意不同两点,依据图象可知,线段AB总是位于A、B两点之间函数图象的上方,因此有结论
的图象上任意不同两点,依据图象可知,线段AB总是位于A、B两点之间函数图象的上方,因此有结论 成立.运用类比思想方法可知,若点
成立.运用类比思想方法可知,若点 图象上的不同两点,则类似地有________________成立.
图象上的不同两点,则类似地有________________成立.
对于大于1的自然数m的三次幂,可用奇数进行以下方式的“分裂”:23= ,33=
,33= ,43=
,43=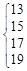 , ,仿此,若m3的“分裂数”中有一个是2015,则m=___________.
, ,仿此,若m3的“分裂数”中有一个是2015,则m=___________.
对于大于1的自然数m的三次幂,可用奇数进行以下方式的“分裂”:23= ,33=
,33= ,43=
,43= , ,仿此,若m3的“分裂数”中有一个是2015,则m=___________.
, ,仿此,若m3的“分裂数”中有一个是2015,则m=___________.
符号 表示不超过
表示不超过 的最大整数,如[
的最大整数,如[ ]=3,
]=3, =-2,定义函数:
=-2,定义函数: ,则下列命题正确的序号是 .
,则下列命题正确的序号是 .
①  ;
;
② 方程 =
= 有无数个解;
有无数个解;
③ 函数 是增函数;
是增函数;
④ 函数 是奇函数.
是奇函数.
⑤ 函数 的定义域为R,值域为[0,1].
的定义域为R,值域为[0,1].
对于以下4个说法:①若函数 在
在 上单调递减,则实数
上单调递减,则实数 ;②若函数
;②若函数 是偶函数,则实数
是偶函数,则实数 ;③若函数
;③若函数 在区间
在区间 上有最大值9,最小值
上有最大值9,最小值 ,则
,则 ;④
;④ 的图象关于点
的图象关于点 对称。其中正确的序号有 。
对称。其中正确的序号有 。
某同学在研究函数 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式 对
对 恒成立; ②函数
恒成立; ②函数 的值域为
的值域为 ;
;
③若 ,则一定有
,则一定有 ; ④函数
; ④函数 在
在 上有三个零点。 其中正确结论的序号有____________.
上有三个零点。 其中正确结论的序号有____________.
给定方程: ,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若
,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若 是该方程的实数解,则
是该方程的实数解,则
 –1.则正确命题是 .
–1.则正确命题是 .