已知函数 (常数
(常数 )在
)在 处取得极大值M=0.
处取得极大值M=0.
(Ⅰ)求 的值;
的值;
(Ⅱ)当 ,方程
,方程 有解,求
有解,求 的取值范围.
的取值范围.
已知 定义域为R,满足:①
定义域为R,满足:① ;
;
②对任意实数 ,有
,有 .
.
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)判断函数的奇偶性与周期性,并求 的值;
的值;
(Ⅲ)是否存在常数 ,使得不等式
,使得不等式 对一切实数
对一切实数 成立.如果存在,求出常数
成立.如果存在,求出常数 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
已知集合 是满足下列性质函数的
是满足下列性质函数的 的全体,在定义域
的全体,在定义域 内存在
内存在 ,使得
,使得 成立。(1)函数
成立。(1)函数 ,
, 是否属于集合
是否属于集合 ?分别说明理由。(2)若函数
?分别说明理由。(2)若函数 属于集合
属于集合 ,求实数
,求实数 的取值范围。
的取值范围。
已知函数 ,
,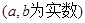 ,
,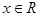 .
.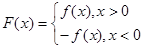
(1)若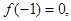 且函数
且函数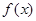 的值域为
的值域为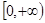 ,求
,求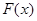 的表达式;
的表达式;
(2)在(1)的条件下,当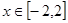 时,
时,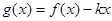 是单调函数,求实数
是单调函数,求实数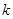 的取值范围;
的取值范围;
(3)设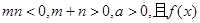 为偶函数,判断
为偶函数,判断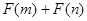 能否大于零?
能否大于零?
已知函数 ,实数a,b为常数),
,实数a,b为常数),
(1)若a=1, 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,判断方程 在(0,1]上解的个数
在(0,1]上解的个数
已知函数 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
(1)如果函数 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值;
的值;
(2)证明:函数 (常数
(常数 )在
)在 上是减函数;
上是减函数;
(3)设常数 ,求函数
,求函数 的最小值和最大值.
的最小值和最大值.
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为H函数.
称为H函数.
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立.
成立.
已知函数 与
与 是定义在
是定义在 上的函数.
上的函数.
(1)试问函数 是否为H函数?并说明理由;
是否为H函数?并说明理由;
(2)若函数 是H函数,求实数a的值;
是H函数,求实数a的值;
(3)在(2)的条件下,若方程 有解,求实数m的取值范围.
有解,求实数m的取值范围.
设函数f (x)的定义域为M,具有性质P:对任意x∈M,都有f (x)+f (x+2)≤2f (x+1).
(1)若M为实数集R,是否存在函数f (x)=ax (a>0且a≠1,x∈R) 具有性质P,并说明理由;
(2)若M为自然数集N,并满足对任意x∈M,都有f (x)∈N. 记d(x)=f (x+1)-f (x).
(ⅰ) 求证:对任意x∈M,都有d(x+1)≤d(x)且d(x)≥0;
(ⅱ) 求证:存在整数0≤c≤d(1)及无穷多个正整数n,满足d(n)=c.
(本题满分12分)若定义在 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件:
①对任意实数 均有
均有 成立;
成立;
② ; ③当
; ③当 时,都有
时,都有 成立。
成立。
(1)求 ,
, 的值;
的值;
(2)求证: 为
为 上的增函数
上的增函数
(3)求解关于 的不等式
的不等式 .
.
(本小题满分14分)
已知二次函数 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1.
⑴ 求此二次函数 的解析式;
的解析式;
⑵ 若函数 的定义域为
的定义域为 =
=  .(其中
.(其中 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数 的值域也为
的值域也为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.