已知函数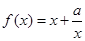
有如下性质：如果常数
，那么该函数在
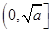上是减函数，在
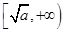上是增函数．
（1）如果函数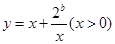
在
上是减函数，在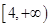
上是增函数，求
的值；
（2）证明：函数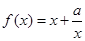（常数）在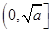上是减函数；
（3）设常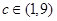数
，求函数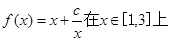
的最小值和最大值．
相关试题
中，底面
是正方形，侧棱
底面
是
的中点．
平面
；
与平面
作圆
的弦
，求弦
的轨迹方程．
两点的圆的方程．
和
的交点，且与直线
平行的直线方程；
中，点
，直线
，设圆
的半径为
，圆心在
上。
上，过点
作圆
，使
，求圆心
的取值范围．相关知识点
推荐套卷
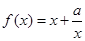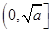已知函数有如下性质：如果常数，那么该函数在上是减函数，在 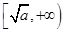上是增函数．
（1）如果函数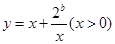在上是减函数，在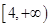上是增函数，求的值；
（2）证明：函数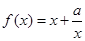（常数）在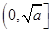上是减函数；
（3）设常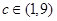数，求函数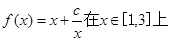的最小值和最大值．
粤公网安备 44130202000953号