设函数f (x)的定义域为M,具有性质P:对任意x∈M,都有f (x)+f (x+2)≤2f (x+1).
(1)若M为实数集R,是否存在函数f (x)=ax (a>0且a≠1,x∈R) 具有性质P,并说明理由;
(2)若M为自然数集N,并满足对任意x∈M,都有f (x)∈N. 记d(x)=f (x+1)-f (x).
(ⅰ) 求证:对任意x∈M,都有d(x+1)≤d(x)且d(x)≥0;
(ⅱ) 求证:存在整数0≤c≤d(1)及无穷多个正整数n,满足d(n)=c.
相关知识点
推荐套卷
 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班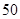 人,吴老师采用
人,吴老师采用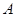 、
、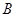 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下: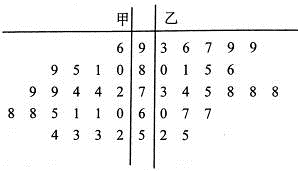
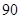 分者为“成绩优秀”.
分者为“成绩优秀”.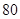 分的成绩中随机抽取
分的成绩中随机抽取 个,记随机变量
个,记随机变量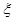 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求 ;
;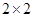 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?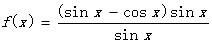 .
. 的定义域和最小正周期;
的定义域和最小正周期; ,若
,若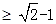 成立,求
成立,求 的取值范围;
的取值范围; ,
,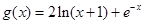 .
. 时,证明:
时,证明: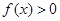 ;
; ,若
,若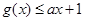 ,求a的取值范围.
,求a的取值范围. 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4, .
. ,
, (
( )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程. 的前
的前 项和为
项和为 ,且满足
,且满足 .
. 的通项公式;
的通项公式; 满足
满足 ,求数列
,求数列 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号