已知偶函数 满足:当
满足:当 时,
时, ,
,
当 时,
时,
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 试讨论:当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点,
有4个零点,
且这4个零点从小到大依次构成等差数列.
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
已知函数
(I)如果对任意 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(II)设函数 的两个极值点分别为
的两个极值点分别为 判断下列三个代数式:
判断下列三个代数式:
① ②
② ③
③ 中有几个为定值?并且是定值请求出;
中有几个为定值?并且是定值请求出;
若不是定值,请把不是定值的表示为函数 并求出
并求出 的最小值.
的最小值.
将函数 的图像向左平移1个单位,再将图像上的所
的图像向左平移1个单位,再将图像上的所
有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数 的图像.
的图像.
(1)求函数 的解析式和定义域;
的解析式和定义域;
(2)求函数 的最大值.
的最大值.
已知函数 ,
, ,且
,且 对
对 恒成立.
恒成立.
(1)求a、b的值;
(2)若对 ,不等式
,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)记 ,那么当
,那么当 时,是否存在区间
时,是否存在区间 (
( ),使得函数
),使得函数 在区间
在区间 上的值域恰好为
上的值域恰好为 ?若存在,请求出区间
?若存在,请求出区间 ;若不存在,请说明理由.
;若不存在,请说明理由.
已知函数 ,
,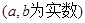 ,
,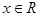 .
.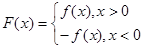
(1)若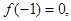 且函数
且函数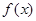 的值域为
的值域为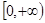 ,求
,求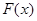 的表达式;
的表达式;
(2)在(1)的条件下,当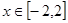 时,
时,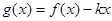 是单调函数,求实数
是单调函数,求实数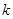 的取值范围;
的取值范围;
(3)设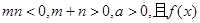 为偶函数,判断
为偶函数,判断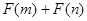 能否大于零?
能否大于零?
(1)已知函数y=ln(-x2+x-a)的定义域为(-2,3),求实数a的取值范围;
(2)已知函数y=ln(-x2+x-a)在(-2,3)上有意义,求实数a的取值范围.
已知集合 是满足下列性质函数的
是满足下列性质函数的 的全体,在定义域
的全体,在定义域 内存在
内存在 ,使得
,使得 成立。(1)函数
成立。(1)函数 ,
, 是否属于集合
是否属于集合 ?分别说明理由。(2)若函数
?分别说明理由。(2)若函数 属于集合
属于集合 ,求实数
,求实数 的取值范围。
的取值范围。