设函数 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,如果函数
上的两个函数,如果函数 在区间
在区间
上有 (
( )个不同的零点,那么称函数
)个不同的零点,那么称函数 和
和 在区间
在区间 上为“
上为“ 阶关联函数”.若
阶关联函数”.若
 与
与 在
在 上是“
上是“ 阶关联函数”,则
阶关联函数”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知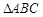 的三内角分别为
的三内角分别为 ,向量
,向量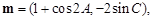
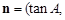
 ,记函数
,记函数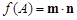 .
.
(1)若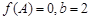 ,求
,求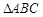 的面积;
的面积;
(2)若关于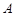 的方程
的方程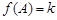 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
若直角坐标平面内两相异点A、B两点满足:① 点A、B都在函数 f (x)的图象上;② 点A、B关于原点对称,则点对 (A,B)是函数 f (x)的一个“姊妹点对”.点对 (A,B)与 (B,A)可看作是同一个“姊妹点对”.已知函数 f (x)=  ,则 f (x)的“姊妹点对”有:
,则 f (x)的“姊妹点对”有:
A.0 个 B.1 个 C.2 个 D.3 个
若直角坐标平面内 两点满足条件:①点
两点满足条件:①点 都在
都在 的图象上;②点
的图象上;②点 关于原点对称,则对称点对
关于原点对称,则对称点对 是函数的一个“兄弟点对”(点对
是函数的一个“兄弟点对”(点对 与
与 可看作一个“兄弟点对”).已知函数
可看作一个“兄弟点对”).已知函数 , 则
, 则 的“兄弟点对”的个数为
的“兄弟点对”的个数为
| A.2 | B.3 | C.4 | D.5 |
对实数a与b,定义新运算“⊗”: .设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A. |
B. |
C. |
D. |
设m是一个非负整数,m的个位数记作 ,如
,如 ,
, ,
, ,称这样的函数为尾数函数.给出下列有关尾数函数的结论:
,称这样的函数为尾数函数.给出下列有关尾数函数的结论:
① ;
;
② ,若
,若 ,都有
,都有 ;]
;]
③ ;
;
则正确的结论的个数为( )
| A.3 | B.2 | C.1 | D.0 |
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则关于函数
为有理数集,则关于函数 有如下四个结论:
有如下四个结论:
① ;
;
②函数 是偶函数;
是偶函数;
③任取一个不为零的有理数 ,
, 对任意的
对任意的 恒成立;
恒成立;
④存在三个点 ,
, ,
, ,使得
,使得 为等边三角形.
为等边三角形.
其中正确结论的个数是( )
A. |
B. |
C. |
D. |
(本小题满分16分)对于函数 ,如果存在实数
,如果存在实数 使得
使得 ,那么称
,那么称 为
为 的生成函数.
的生成函数.
(1)下面给出两组函数, 是否分别为
是否分别为 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: ;
;
第二组: ;
;
(2)设 ,生成函数
,生成函数 .若不等式
.若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
已知函数 ,
, .定义:
.定义: ,
, ,……,
,……,
 ,
, …满足
…满足 的点
的点 称为
称为 的
的 阶不动点.则
阶不动点.则 的n
的n
阶不动点的个数是( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
若函数 满足对任意的
满足对任意的 ,都有
,都有 成立,则称函数
成立,则称函数 在区间
在区间 上是“被
上是“被 约束的”。若函数
约束的”。若函数 在区间
在区间 上是“被
上是“被 约束的”,则实数
约束的”,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |