设函数f (x)= x-lnx (x>0),则y=f (x)( )
x-lnx (x>0),则y=f (x)( )
A.在区间(  ,1)、(1,e)内均有零点 ,1)、(1,e)内均有零点 |
B.在区间(  ,1)、(1,e)内均无零点 ,1)、(1,e)内均无零点 |
C.在区间(  ,1)内有零点,在区间(1,e)内无零点 ,1)内有零点,在区间(1,e)内无零点 |
D.在区间(  ,1)内无零点,在区间(1,e)内有零点 ,1)内无零点,在区间(1,e)内有零点 |
函数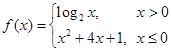 ,若实数
,若实数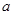 满足
满足 =1,则实数
=1,则实数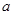 的所有取值的和为( )
的所有取值的和为( )
| A.1 | B. |
C. |
D.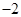 |
已知函数 (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若函数 在
在 上无零点,求
上无零点,求 的最小值;
的最小值;
(3)若对任意的 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
已知函数 在
在 处取得极值.
处取得极值.
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;
(3)证明:对任意的正整数 ,不等式
,不等式 …
… 都成立.
都成立.