湖北省荆门市高二下学期期末质量检测理科数学试卷
要完成下列2项调查:
①从某社区125户高收入家庭,280户中等收入家庭,95户低收入家庭中选出100户调查社会购买力的某项指标;
②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况.
应采用的抽样方法是
| A.①用随机抽样法②用系统抽样法 |
| B.①用分层抽样法②用随机抽样法 |
| C.①用系统抽样法②用分层抽样法 |
| D.①、②都用分层抽样法 |
打靶时,甲每打10次可中靶8次,乙每打10次可中靶7次.若2人同时射击一个目标,则他们都中靶的概率是
A. |
B. |
C. |
D. |
若数列 满足
满足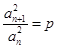 (
( 为正常数,
为正常数,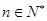 ),则称
),则称 为“等方比数列”.
为“等方比数列”.
甲:数列 是等方比数列;乙:数列
是等方比数列;乙:数列 是等比数列,则
是等比数列,则
| A.甲是乙的充分条件但不是必要条件 |
| B.甲是乙的必要条件但不是充分条件 |
| C.甲是乙的充要条件 |
| D.甲既不是乙的充分条件也不是乙的必要条件 |
已知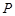 是正四面体
是正四面体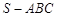 的面
的面 上一点,
上一点,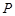 到面
到面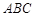 的距离与到点
的距离与到点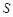 的距离相等,则动点
的距离相等,则动点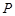 的轨迹所在的曲线是
的轨迹所在的曲线是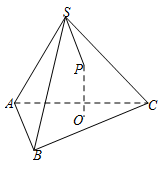
| A.圆 | B.抛物线 | C.双曲线 | D.椭圆 |
要排出某班一天中语文、数学、政治、英语、体育、艺术6门课各一节的课程表,要求数学课排在前3节,英语课不排在第6节,则不同的排法种数为 .(以数字作答)
若第一象限内的动点 满足
满足 ,则以P为圆心,R为半径且面积最小的圆的方程为__ ___.
,则以P为圆心,R为半径且面积最小的圆的方程为__ ___.
对于三次函数 给出定义:设
给出定义:设 是函数
是函数 的导函数,
的导函数, 是
是 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点” .某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心.
的“拐点” .某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心.
给定函数 ,请你根据上面探究结果,解答以下问题:
,请你根据上面探究结果,解答以下问题:
(1)函数 的对称中心为 ;
的对称中心为 ;
(2)计算 …
… .
.
在二项式 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列.
(1)求展开式中的常数项;
(2)求展开式中各项的系数和.
如图,四边形 是矩形,
是矩形, 平面
平面 ,四边形
,四边形 是梯形,
是梯形, ,
, , 点
, 点 是
是 的中点,
的中点, .
.
(1)求证: ∥平面
∥平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
在我市“城乡清洁工程”建设活动中,社会各界掀起美化环境的热潮.某单位计划在小区内种植A,B,C,D四棵风景树,受本地地理环境的影响,A,B两棵树成活的概率均为 ,C,D两棵树成活的概率为
,C,D两棵树成活的概率为 ,用
,用 表示最终成活的树的数量.
表示最终成活的树的数量.
(1)若A,B两棵树有且只有一棵成活的概率与C,D两棵树都成活的概率相等,求 的值;
的值;
(2)求 的分布列(用
的分布列(用 表示);
表示);
(3)若A,B,C,D四棵树中恰有两棵树成活的概率最大,求 的范围.
的范围.
已知 分别是椭圆
分别是椭圆 的左、右焦点,其左准线与x轴相交于点N,并且满足
的左、右焦点,其左准线与x轴相交于点N,并且满足 .设A、B是上半椭圆上满足
.设A、B是上半椭圆上满足 的两点,其中
的两点,其中 .
.
(1)求此椭圆的方程;
(2)求直线AB的斜率 的取值范围.
的取值范围.
 等于
等于



 、
、 、
、 三个单位向量两两之间夹角为60°,则
三个单位向量两两之间夹角为60°,则


 上任一点
上任一点 处的切线斜率
处的切线斜率 ,则该函数
,则该函数 的单调递减区间为
的单调递减区间为




 …
…
 …
…
 …
…
 …
…
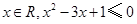 ”的否定是
”的否定是 

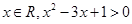
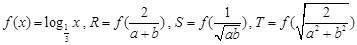 ,a,b为正实数,则
,a,b为正实数,则 的大小关系为
的大小关系为
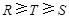

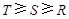
 的图象如图所示,则它与
的图象如图所示,则它与 轴所围图形的面积为 .
轴所围图形的面积为 . 
 …
… .所有这些椭圆都以
.所有这些椭圆都以 为准线,离心率
为准线,离心率 …
… .
. ;
; 对任意的
对任意的 恒成立,求a的取值范围.
恒成立,求a的取值范围. 在
在 处取得极值.
处取得极值. 的值;
的值;  的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; ,不等式
,不等式 …
… 都成立.
都成立. 粤公网安备 44130202000953号
粤公网安备 44130202000953号