(本题16分)已知函数 ,其中e是自然数的底数,
,其中e是自然数的底数, ,
,
(1)当 时,解不等式
时,解不等式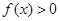 ;
;
(2)若当 时,不等式
时,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)当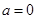 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程 在
在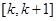
上有解?若存在,请写出所有可能的k的值;若不存在,说明理由。
如图是一个半圆形湖面景点的平面示意图.已知 为直径,且
为直径,且 km,
km, 为圆心,
为圆心, 为圆周上靠近
为圆周上靠近 的一点,
的一点, 为圆周上靠近
为圆周上靠近 的一点,且
的一点,且 ∥
∥ .现在准备从
.现在准备从 经过
经过 到
到 建造一条观光路线,其中
建造一条观光路线,其中 到
到 是圆弧
是圆弧 ,
, 到
到 是线段
是线段 .设
.设 ,观光路线总长为
,观光路线总长为 .
.
(1)求 关于
关于 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
设函数 ,若
,若 的图象与
的图象与 图象有且仅有两个不同的公共点
,则下列判断正确的是()
图象有且仅有两个不同的公共点
,则下列判断正确的是()
| A. | 当 时, |
| B. | 当 时, |
| C. | 当 时, |
| D. | 当 时, |
已知定义在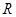 上的函数
上的函数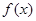 的图象是连续不断的,且有如下对应值表:
的图象是连续不断的,且有如下对应值表:
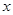 |
1 |
2 |
3 |
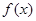 |
6.1 |
2.9 |
-3.5 |
那么函数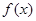 一定存在零点的区间是 ( )
一定存在零点的区间是 ( )
A.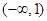 B.
B.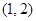 C.
C.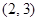 D.
D.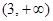
已知定义在R上的函数 且
且 .若方程
.若方程 有三个不相等的实数根,则实数k的取值范围是( )
有三个不相等的实数根,则实数k的取值范围是( )
A. |
B. |
C. |
D. |
已知函数 其中e表示自然对数的底数.
其中e表示自然对数的底数.
(1)若g(x)=m有零点,求m的取值范围;
(2)确定t的取值范围,使得g(x)-f(x)=0有两个相异实根.
奇函数f(x)、偶函数g(x)的图像分别如图1、2所示,方程f(g(x))=0,g(f(x))=0的实根个数分别为a、b,则a+b=( )

| A.14 | B.10 | C.7 | D.3 |
已知函数 ,
, ,
, .
.
(1)若函数 在区间
在区间 内恰有两个零点,求实数
内恰有两个零点,求实数 的取值范围;
的取值范围;
(2)若 ,设函数
,设函数 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 ,记
,记 ,求函数
,求函数 在区间
在区间 上的最小值.
上的最小值.