已知二次函数f(x)=ax2+bx+c .
(1)设集合A={x|f(x)=x}.
①若A={1,2},且f(0)=2,求f(x)的解析式;
②若A={1},且a≥1,求f(x)在区间[﹣2,2]上的最大值M(a).
(2)设f(x)的图像与x轴有两个不同的交点,a>0, f(c)=0,且当0<x<c时,f(x)>0.用反证法证明: .
.
已知 在
在 时有极值0。
时有极值0。
(1)求常数 a,b的值;
(2)求f(x)的单调区间。
(3)方程f(x)=c在区间[-4,0]上有三个不同的实根时实数 的范围。
的范围。
(本小题满分13分)已知函数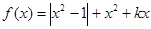 .
.
(1)若对于区间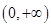 内的任意
内的任意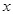 ,总有
,总有 成立,求实数
成立,求实数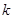 的取值范围;
的取值范围;
(2)若函数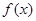 在区间
在区间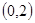 内有两个不同的零点
内有两个不同的零点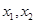 ,求:
,求:
①实数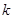 的取值范围; ②
的取值范围; ②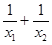 的取值范围.
的取值范围.
已知函数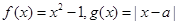 .
.
(1)当 时,求
时,求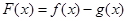 的零点;
的零点;
(2)若方程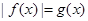 有三个不同的实数解,求
有三个不同的实数解,求 的值;
的值;
(3)求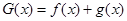 在
在 上的最小值
上的最小值 .[来
.[来
已知 ,函数
,函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的最小值;
的最小值;
(Ⅱ)当 时,讨论
时,讨论 的图象与
的图象与 的图象的公共点个数.
的图象的公共点个数.