(本小题满分12分)已知函数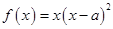 ,
,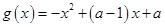 (其中
(其中 ).
).
(Ⅰ)如果函数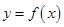 和
和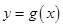 有相同的极值点,求
有相同的极值点,求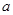 的值,并直接写出函数
的值,并直接写出函数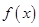 的单调区间;
的单调区间;
(Ⅱ)令 ,讨论函数
,讨论函数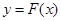 在区间
在区间 上零点的个数。
上零点的个数。
对于函数 ,如果存在实数
,如果存在实数 、
、 使得
使得 ,那么称
,那么称 为
为 的生成函数.
的生成函数.
(1)下面给出两组函数, 是否为
是否为 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: ;
;
第二组: .
.
(2)设 ,
, ,
, ,生成函数
,生成函数 ,若不等式
,若不等式 在
在 上有解,求实数t的取值范围.
上有解,求实数t的取值范围.
已知函数 .
.
(1)求 的单调区间和极值点;
的单调区间和极值点;
(2)求使 恒成立的实数
恒成立的实数 的取值范围;
的取值范围;
(3)当 时,是否存在实数
时,是否存在实数 ,使得方程
,使得方程 有三个不等实根?若存在,求出
有三个不等实根?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
已知函数 是偶函数.
是偶函数.
(1)求k的值;
(2)若函数y=f(x)的图象与直线 没有交点,求b的取值范围.
没有交点,求b的取值范围.
(3)设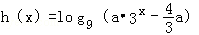 ,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
已知函数 且
且 .
.
(Ⅰ) 若1是关于x的方程 的一个解,求t的值;
的一个解,求t的值;
(Ⅱ) 当 且
且 时,解不等式
时,解不等式 ;
;
(Ⅲ)若函数 在区间(-1,2]上有零点,求t的取值范围.
在区间(-1,2]上有零点,求t的取值范围.
已知函数 (
( 为自然对数的底数,
为自然对数的底数, ).
).
(1)判断曲线 在点
在点 处的切线与曲线
处的切线与曲线 的公共点个数;
的公共点个数;
(2)当 时,若函数
时,若函数 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
已知函数 .
.
(Ⅰ)当 时,证明:
时,证明: 为奇函数;
为奇函数;
(Ⅱ)若关于 的方程
的方程 有两个不等实数根,求实数
有两个不等实数根,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数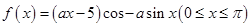 ,其中
,其中 为正实数。
为正实数。
(1)当 时,求
时,求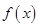 在
在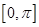 上的零点个数。
上的零点个数。
(2)对于定义域内的任意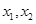 ,将
,将 的最大值记作
的最大值记作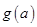 ,求
,求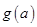 的表达式。
的表达式。